Тепловые двигатели, это тепловая машина, превращающая тепло в механическую энергию, использует зависимость теплового расширения вещества от температуры. Обычно работа совершается за счет изменения объема вещества, но иногда используется изменение формы рабочего тела (в твердотельных двигателях). Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие разницы температур, производится нагревание рабочего тела (газа), который совершает работу за счет изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем (например, при сжигании топлива) и охладителем, в роли которой используется окружающая среда.

 

 

Принцип действия и концепция

 

Двигатели внутреннего сгорания классифици­руются как тепловые двигатели. Существенной особенностью теплового двигателя является прямой термодинамический цикл, который характеризуется совершением работы.

В отличие от тепловых двигателей тепловые насосы, также называемые холодильными машинами, характеризуются обратным тер­модинамическим циклом, т.е. требуют для своей работы внешнего привода.

Принцип действия тепловых двигателей всегда один и тот же. Рабочая среда сжима­ется с подводом энергии и соответствующим увеличением давления. За этим следует рас­ширение, сопровождаемое совершением работы. В разомкнутых циклах среда, совер­шившая работу, выпускается наружу. В замкнутых циклах начальное состояние должно быть восстановлено путем охлаждения рабо­чей среды перед началом сжатия.

Многие тепловые двигатели характеризу­ются подводом энергии в процессе сгорания топлива (табл. «Характеристики и принцип действия тепловых двигателей» ). Во время сгорания топлива химически связанная в топливе энергия вы­деляется в виде тепла, необходимого для совершения цикла. В процессе горения про­исходит соединение веществ, содержащих углерод и водород, с кислородом (окисле­ние), поэтому воздух с объемным содержа­нием кислорода приблизительно 21% со­ставляет значительную часть рабочей среды.

 

 

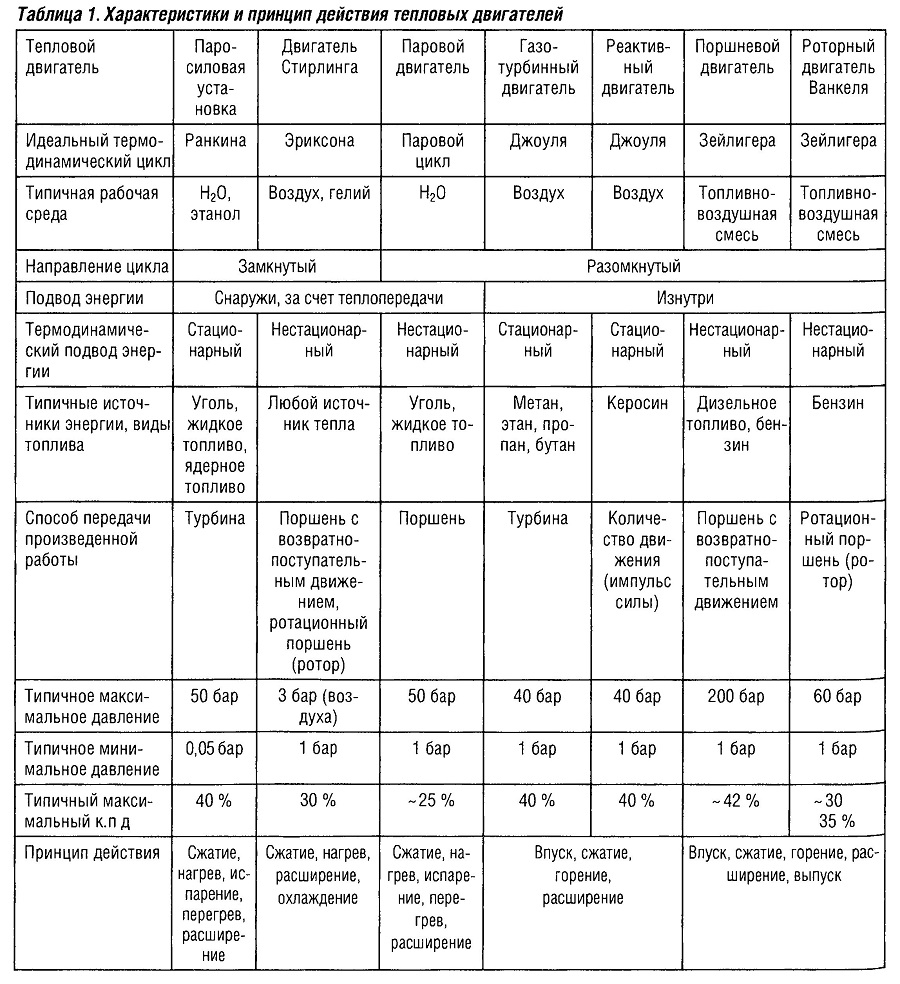
Направление цикла подвода энергии

 

Важным фактором, определяющим на­правление цикла, является способ подвода энергии. Здесь различаются стационарный (непрерывный) и нестационарный (цикличе­ский) подвод энергии. Для всех поршневых двигателей, включая двигатель Стирлинга, характерен нестационарный подвод энергии, который происходит, когда поршень нахо­дится в верхней мертвой точке такта сжатия, и объем цилиндра минимален.

Характерным для всех разомкнутых ци­клов является внутренний подвод энергии, достигаемый за счет подачи и сжигания топлива. В противоположность этому зам­кнутые циклы требуют подвода энергии че­рез теплообменники. Здесь прямой контакт рабочей среды с продуктами горения, если не учитывать теплопроводность, отсутствует. Уникальным в этом отношении является па­ровой двигатель, в котором рабочая среда испаряется под действием теплового потока, создаваемого внешним источником, а затем поступает в поршневой двигатель.

Тепловые двигатели также различаются в отношении используемых источников энер­гии. Используются источники энергии трех видов: твердые, жидкие и газообразные. Главное преимущество тепловых двигателей, работающих по принципу разомкнутого цикла с внутренним подводом энергии, состоит в том, что они не требуют теплообменников для обеспечения требуемого направления цикла и, следовательно, имеют более компактную конструкцию. Это преимущество может быть проявлено в еще большей степени за счет применения жидкого топлива с высокой плотностью энергии. Газовые двигатели для легковых и коммерческих автомобилей также становятся все более привлекательными (благодаря низким эксплуатационным за­тратам и относительно небольшому расходу топлива). Таким образом, двигатели внутрен­него сгорания являются наиболее совершен­ными из тепловых двигателей.

 

КПД дигателя внутреннего сгорания

 

Двигатель внутреннего сгорания хактеризуется разомкнутым циклом и внутренним сгоранием топлива. Нестационарный ре­жим подвода энергии позволяет получить температуру рабочей среды, усредненную по массе, на тактах впуска и сжатия свыше 2500 К и усредненные пиковые давления свыше 200 бар с очень хорошим к.п.д., свыше 40%.

В двигателях со стационарным циклом ограничения, налагаемые свойствами мате­риалов, не позволяют достигнуть давлений и температур такого порядка. В них дости­гаются только локальные пиковые темпе­ратуры около 2500 К. Поэтому, например, газовые турбины имеют более низкий к.п.д. Паровые турбины с замкнутым циклом до­стигают более высокого КПД, чем газовые, при умеренном давлении около 50 бар. Это достигается за счет значительного снижения уровня низкого давления. Максимальный КПД прочих тепловых двигателей значи­тельно ниже.

 

Двигатель внутреннего сгорания с возвратно-поступательным движением поршней

 

Двигатель внутреннего сгорания в его порш­невом варианте является основным типом теплового двигателя, используемого в автомобилестроении. В поршневом двигателе возвратно поступательное движение порш­ней преобразуется во вращение коленчатого вала. В принципе двигатели могут работать на самых различных видах топлива, однако на сегодняшний день основными источниками энергии для них остаются дизельное топливо и бензин.

 

Рабочие циклы двигателя

 

Основные принципы

 

Цикл представляет собой термодинамиче­ский процесс, имеющий идентичные началь­ное и конечное состояния. Обычно цикл про­ходит через несколько изменений состояния, сопровождающихся совершением тепловым двигателем работы. При этом рабочая среда цикла претерпевает термодинамические из­менения состояния.

Изменения состояния (см. Термодинамика) различаются в отношении того, совершается работа W в форме работы при изменении объема ∫pdV или имеет место теплообмен с окружающей средой Q=∫TdS. Диаграмма «давление-объем» (диаграмма p-V, рис. «Иллюстрация термодинамического цикла при помощи диаграммы p-V» ) демонстрирует, производится ли работа и в каком количестве, в то время как диаграмма «температура-энтропия» (диаграмма T-S, рис.  «Иллюстрация термодинамического цикла при помощи диаграммы T-S» ) иллюстрирует теплообмен, проис­ходящий в замкнутой системе.

 

 

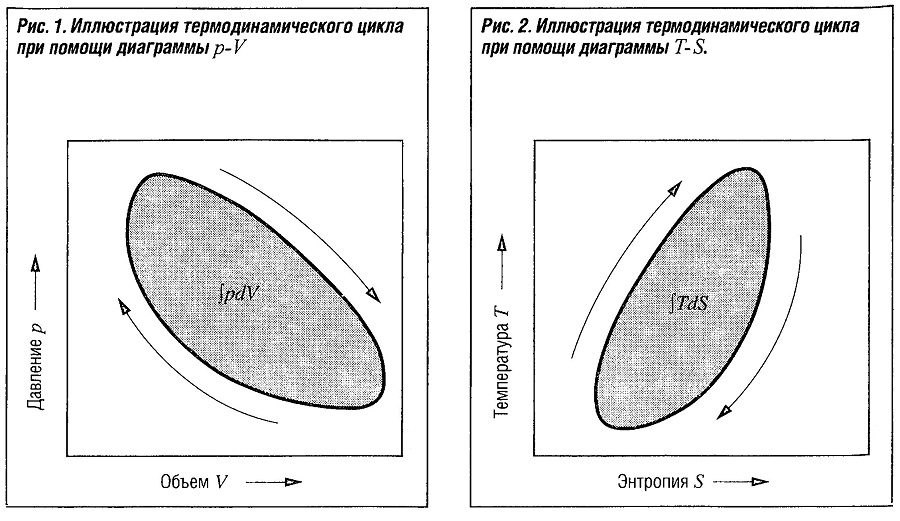
Интеграл работы при изменении объема ∫pdV можно интерпретировать на диаграмме p-V, как площадь, заключенную между лини­ями изменения состояния. Если цикл направ­лен вправо, по часовой стрелке, т.е. область располагается справа от линии изменения состояния, интеграл является в математи­ческом смысле положительным. При этом цикл совершает работу. Рабочие циклы холо­дильных машин и компрессоров направлены влево, т.е. против часовой стрелки.

В дополнение к термину «работа при изме­нении объема» ∫pdV, который обычно ис­пользуется применительно к двигателям вну­треннего сгорания, существует также термин «техническая работа»

W_t=∫Vdp,

который ча­сто используется применительно к машинам с непрерывным потоком рабочей среды, та­ким как газовые турбины. Из интерпретации работы, как площади на диаграмме р-V, ясно, что обе формы работы в иллюстрируемом цикле в отношении количества идентичны.

Для совершения в цикле работы должен иметь место подвод тепла. В обратимом ци­кле (без энергии рассеивания Е_d) количество добавленного тепла

Q=∫TdS

равно инте­гралу температуры по изменению энтропии. На диаграмме Т-S количество тепла, добав­ленного в замкнутом цикле, соответствует замкнутой площади (рис. «Иллюстрация термодинамического цикла при помощи диаграммы T-S» ).

В соответствии с первым законом термо­динамики (см. «Термодинамика»):

∫dU=∫TdS+∫dE_a-∫pdV,

где U означает энергию.

Для обратимого цикла с идентичными начальной и конеч­ными точками ∫dU=0. Количество тепла, подведенного к циклу, должно создаваться, в то время как рассеиваемое тепло возвраща­ется неиспользуемым в окружающую среду. К.п.д. цикла, следовательно, определяется, как отношение общей произведенной работы W (сумма работ, совершенных подведенным и рассеянным теплом) к количеству добавлен­ного тепла Q_add:

η_th = W/Q_add = |∫pdV | / Q_add

 

Идеальный цикл Карно

 

Поскольку каждый цикл, сопровождающийся совершением работы, предполагает подвод тепла, в ходе цикла также имеет место изменение температуры. В 1824 году Николя Леонард Сади Карно описал изменения со­стояния в цикле, который достигает мак­симального к.п.д. между двумя данными температурными пределами. Поскольку наилучший к.п.д. может быть достигнут при отсутствии рассеивания тепла, подвод и рас­сеивание тепла должны происходить изотер­мически. Идеальным для совершения работы является адиабатический цикл. Цикл Карно, следовательно, состоит из изотермического поглощения и рассеивания тепла и изоэнтро- пического (адиабатического и обратимого) сжатия и расширения (рис. «Цикл Карно» ).

 

 

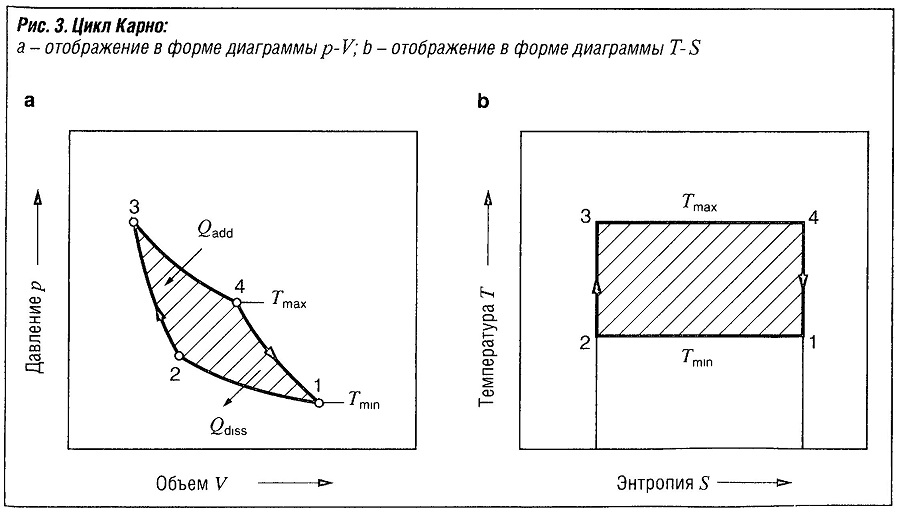
Применяя первый закон термодинамики, можно сделать вывод, что при изотермиче­ском изменении состояния идеального газа внутренняя энергия остается неизменной, а работа равна количеству добавленного тепла. При этом применимо следующее выражение:

∫dU = ∫TdS — ∫pdV = 0.

При адиабатическом изменении состояния работа эквивалентна изменению внутренней энергии и, соответственно, температуры. При этом применимо следующее выражение:

∫dU=0 — ∫pdV.

Для к.п.д. может быть выведено выражение

η_с = W/Q_{add =} (Q_add—Qdiss) / Q_{add = (Tmax-Tmin) / Tmax}

Этот тепловой КПД является максималь­ным КПД, который может быть получен на машине, работающей в диапазоне двух температурных пределов. Никакой другой цикл не достигает к.п.д. такого уровня. Од­нако на практике выясняется, что работа, произведенная при данном изменении объема V_max-V_min, мала, и для достиже­ния плотности энергии, сравнимой с дру­гими циклами, требуются очень высокие пиковые давления р_max. Даже обеспечение практически изотермической теплопере­дачи затруднено, поскольку это требует применения больших теплообменников.

Отсюда следует, что в контексте тепловых двигателей этот цикл имеет скорее теорети­ческое значение, однако он играет важную роль в рассмотрении эксергии (максималь­ной работы, которая может быть получена при данном уровне энергии) и анэргии (энер­гии, которая не может быть использована), а также в отношении тепловых насосов и холодильных установок.

 

Основные циклы поршневых двигателей внутреннего сгорания

 

Поскольку фазы расширения и сжатия в двигателях с возвратно-поступательным движением поршней могут быть описаны адиабатической кривой, различные циклы отличаются способом подвода тепла. Про­цесс газообмена (цикл нагнетания) обычно заменяется теплообменом с окружающей средой (в целях упрощения предполагается, что процесс протекает при постоянной массе) для замыкания цикла.

Можно предположить, что подвод тепла в форме высвобождения химически связанной энергии («высвобождения тепла» или «про­цесса горения») может быть относительно медленным или очень быстрым. В цикле при постоянным объеме предполагается, что все тепло высвобождается в верхней мертвой точке (ВМТ) поршня за бесконечно малое время. Это изменение состояния может быть описано циклом при постоянном объеме.

Если высвобождение тепла происходит в течение конечного времени, можно предпо­ложить, что имеет место цикл при постоян­ном давлении. Здесь снижение давления вследствие расширения компенсируется по­вышением давления вследствие подвода тепла во время горения топлива.

Комбинация циклов при постоянном дав­лении и постоянном объеме представляет собой цикл Зейлигера при предельном дав­лении, посредством которого была сделана попытка приблизиться к реальному процессу сгорания топлива в поршневых двигателях.

 

Идеальный термодинамический цикл сгора­ния (цикл при постоянном объеме)

 

Предполагается, что подвод тепла в верхней мертвой точке осуществляется мгновенно и может быть описан, как изохорическое изме­нение состояния (рис. 2—>3, «Идеальные циклы при постоянном объеме» ). Цикл заряда (4—>1) моделируется в упрощенной форме изохорическим рассеиванием тепла в окру­жающую среду. Таким образом, в течение этих двух фаз работа с изменением объема не производится:

W=∫pdV=0.

 

 

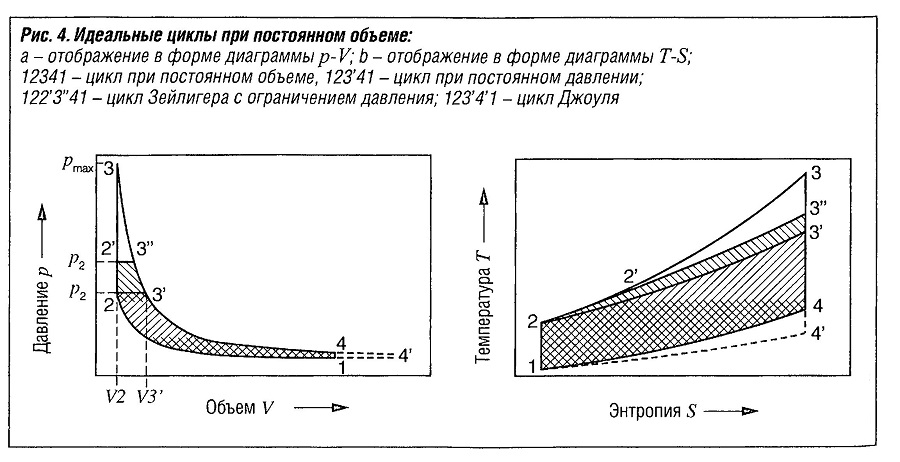
Сжатие (1—>2) и расширение (3—>4) рас­сматриваются как адиабатические процессы. Применение к этим двум фазам первого за­кона термодинамики дает dU= pdV, т.е. W12=mc_v(T₂— Т₁), a W₃₄= mc_v(T₄— Т₃) от­носится к произведенной работе.

В соответствии с первым законом термо­динамики dU = TdS на стадии 2—>3, а коли­чество добавленного тепла

Q₂₃ = mc_v(T₃ — Т₂).

Таким образом КПД η_th может быть опреде­лен как:

 η_th = |∑W|/ Q_add = T₁— Т₂ + T₃— Т₄ / T3- Т2

где подвод тепла осуществляется на протя­жении всех стадий цикла, a Q_add обозначает количество добавленного тепла. Предпола­гая, что расширение и сжатие являются адиа­батическими, можно показать, что:

Т₄ / T₁ = Т₃ / T₂

Таким образом, в целях упрощения:

η_th = 1 — Т₁ / T₂ = 1-ε^1-k

Предполагается, что теплоемкости во время сжатия и расширения идентичны. Этот спо­соб выведения КПД из степени сжатия ε и изоэнтропической экспоненты к предпола­гает, что газ является идеальным.

 

 

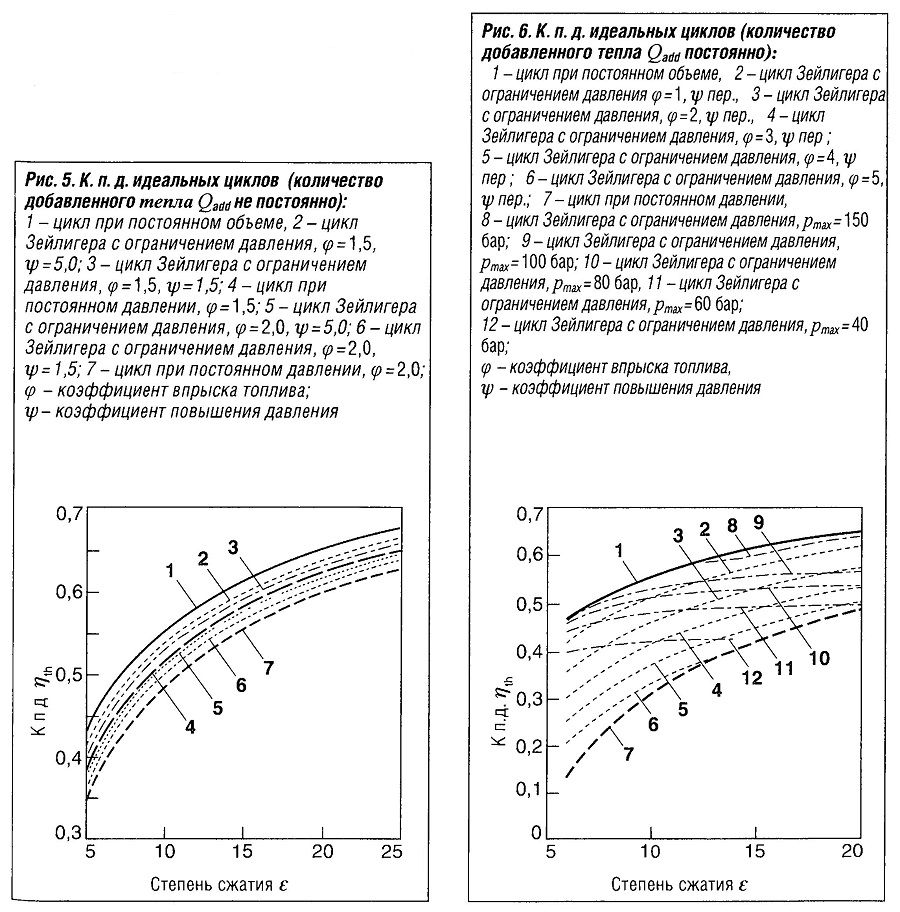
При увеличении степени сжатия к.п.д. воз­растает (рис. «КПД идеальных циклов» ). В бензиновых двигателях степень сжатия ограничивается детонацией. Обычно для бензиновых двигателей с атмос­ферным всасыванием воздуха коэффициент сжатия составляете ε=10-12, а максимальное давление — приблизительно 60 бар. Двигатели с турбонаддувом, вследствие ограничений, связанных с детонацией, имеют более низкую степень сжатия, равную ε =9-10. При этом до­стигаются пиковые давления до 120 бар. Двига­тели с прямым впрыском топлива и послойным распределением заряда топлива имеют степень сжатия ε > 12; при частичной нагрузке потен­циал степени сжатия составляет даже до ε=14.

Двигатель Стирлинга (Роберт Стирлинг, 1816 ) может работать в соответствии с принципом и переменного рабочего объема, но в своих реализованных формах изменений состояния демонстрирует сходство с циклами при постоянном объеме. Фазы адиабатического сжатия и расширения, однако, характеризуются изотермическими линиями. В принципе, это дает высокий КПД, идентичный КПД цикла Карно.

 

Цикл при постоянном давлении

 

Естественно предположить, что для дости­жения высокой мощности процессы подвода и высвобождения тепла должны быть изо­барическими (рис. «Идеальные циклы при постоянном объеме» ). Этот цикл обычно ис­пользуется в дизельных двигателях, которые ограничены в отношении пикового давления и работают с конечной продолжительностью впрыска топлива и распространения пламени. Цикл заряда (4—>1) снова моделируется в упрощенной форме, как рассеивание тепла в окружающую среду. Процессы сжатия (1—>2) и расширения(3—>4) рассматриваются как адиабатические. Здесь применимы те же по­ложения, которые были указаны для цикла при постоянном объеме.

 

Изобарическое изменение

 

Во время изобарического изменения со­стояния имеет место как подвод тепла, так и выполнение работы (2—>3). В качестве ха­рактеристического значения количества подведенного тепла используется объем в конце изобарического изменения состояния, называемый «объемом впрыснутого топлива» V3 (рис. «Идеальные циклы при постоянном объеме» ), и определяется «ко­эффициент впрыска» φ = V₃/V₂. Однако, его не следует путать с количеством впрыс­нутого топлива.

В соответствии с первым законом термо­динамики, dU = TdS-pdV на стадии 2—>3 и для количества добавленного тепла:

Q₂₃ = mc_v (T3 — T2)+ p_max(V3 — V2).

Таким образом, к.п.д. может быть определен как

η_th = ε^1-k/ (φ^к — 1)/(φ-1).

Предположения аналогичны сделанным для цикла при постоянном объеме. КПД, дости­жимый при такой же степени сжатия, ниже, чем для цикла при постоянном объеме. Од­нако, поскольку дизельные двигатели рабо­тают с более высокой степенью сжатия, и их КПД в общем случае выше (см. рис. «КПД идеальных циклов» ). Следовательно, при разработке дизельных двигателей следует стремиться к получению высокого пикового давления.

Максимальные допустимые пиковые давления для двигателей легковых ав­томобилей составляют около 180 бар, а для двигателей коммерческих автомоби­лей — более 220 бар. Степень сжатия для процессов прямого впрыска топлива, при­меняемых в настоящее время, составляет ε = 16 -19. В случае запаздывания впрыска конечное давление сжатия фактически соот­ветствует пиковому давлению, и дизельный цикл имеет сходство с циклом при постоян­ном давлении с φ = 9.

 

Цикл Зейлигера с ограничением давления

 

В 1922 году Мирон Зейлигер описал ком­бинацию циклов при постоянном объеме и давлении (рис.5). Процедура вывода здесь опущена.

Введя «коэффициент повышения давле­ния» ψ = p₂‘/ p₂ можно вывести для к.п.д. следующее соотношение:

η_th = 1 — ε^1-k(ψk — 1)/ ψ — 1 + kψ ( φ-1)

Значение к.п.д., как и ожидалось, лежит между к.п.д. циклов при постоянном давле­нии и при постоянном объеме (рис. «КПД идеальных циклов» ).

 

Турбодвигатели: идеальный цикл

 

Турбодвигатели, в особенности газовые тур­бины и, следовательно, двигатели с турбо­нагнетателями отработавших газов работают при постоянном массовом расходе, а не в прерывистом режиме, как поршневые дви­гатели. Соответствующий идеальный цикл был впервые описан Джеймсом Прескопом Джоулем около 1840 г., как калорический двигатель без потерь.

Предполагается, что процессы сжатия и расширения в крыльчатке компрессора и рабочем колесе турбины являются адиабати­ческими. Также предполагается, что за счет наличия камеры сгорания с постоянным по­током сгорание топлива представляет собой изобарический подвод тепла. В отличие от цикла при постоянном давлении с конечным расширением («расширением отсечки»), за счет выбранного принципа поршня, в цикле Джоуля расширение происходит до дости­жения давления окружающей среды (рис.  «Идеальные циклы при постоянном объеме» ).

Таким образом, теоретически может быть получено более высокое значение работы, и КПД становится идентичен КПД цикла при постоянном объеме. Введя коэффициент давления  П = p₂/p₁ = p_max / p_1,получаем следующее соотношение для КПД:

η_th = 1 — T₁/T₂ = 1 — П^(k-1)/k

В зависимости от коэффициента давления П КПД может иметь высокие значения. Однако, когда дело касается реальных тур­бодвигателей, на коэффициент давления налагаются определенные ограничения (см. «Турбонагнетатели отработавших газов»). По этой причине газовые турбины часто делают многоступенчатыми, и высокая плотность мощности достигается в них за счет высокого массового расхода топлива.

 

Реальные циклы

 

Идеальные циклы подходят для демонстра­ции базовых соотношений. В случае новых двигателей с пока что неизвестными характеристиками они помогают рассмотреть принцип действия и оценить КПД. Однако, для детального анализа требуется выполнить расчет реального цикла.

Реальные циклы отличаются от идеаль­ных. Различия заключаются в том, что те­плоемкости рассматриваются зависимыми от температуры или давления. Измененный химический состав отработавших газов также аппроксимируется в виде соответствующих переменных с целью учета изменений физи­ческих свойств в процессе сгорания топлива. В частности, предполагается, что имеет ме­сто не адиабатическое изменение состояния, а как минимум, одна политропная кривая с экспонентой, адаптированной к тепловым потерям, или даже имеют место тепловые потери через стенки цилиндра, например при использовании подхода Вошни, в соот­ветствии с теорией подобия Рейнольдса.

Цикл заряда рассчитывается с учетом по­терь рассеивания (потерь потока и реальных сечений потока, см. «Гидромеханика») и также учитывается влияние остаточных отра­ботавших газов. В отношении трения обычно используются эмпирические подходы, а теплотворная способность топлива вы­числяется в зависимости от коэффициента избытка воздуха. В конечном итоге осущест­вляется детальное моделирование процессов подвода тепла (сгорания топлива и нагрева) и рассеивания тепла (теплопередачи).

Важным и простым способом быстрой оценки реального цикла является его описа­ние в форме цепочки КПД. Здесь реальные циклы отображаются последовательно с уче­том отдельных характеристических величин. Примером такой характеристической вели­чины может служить механический КПД.

 

Общий коэффициент полезного действия

 

Общий или эффективный КПД η_eff опреде­ляет количество эффективной энергии P_eff относительно энергии Q_add = m_B Н_U, которая была подведена при массовом расходе топлива m_B и его низшей теплотворной способности Н_U

η_{eff = Peff / Qadd}

При высоких нагрузках дизельные двига­тели имеют эффективный к.п.д. до 45%; эффективный к.п.д. больших, тихоходных дизельных двигателей значительно выше. Эффективный к.п.д. бензиновых двигателей в лучшем случае может достигать 40%.

 

Механический коэффициент полезного действия

 

Механический КПД представляет собой от­ношение эффективной мощности P_eff к номи­нальной мощности Р_ind. Номинальная мощ­ность определяется из работы W (площадь характеристики ∫pdV для реального цикла) и времени t за один рабочий цикл, в соответ­ствии со следующим соотношением:

Р_ind = dW/dt ≈ ΔW/Δt

Эффективная мощность отличается от но­минальной мощности в основном учетом по­терь на трение (в поршнях и подшипниках), потерь мощности в элементах управления (распределительный вал, клапаны), во вспо­могательных агрегатах (масляный и водяной насосы, топливный насос, генератор). Для механического КПД:

η_m = P_eff / Р_ind

Обычно механический КПД зависит от на­грузки и при полной нагрузке может дости­гать 90%, в то время как при низкой нагрузке (10%) регистрируются значения около 70%.

 

Фактор эффективности цикла

 

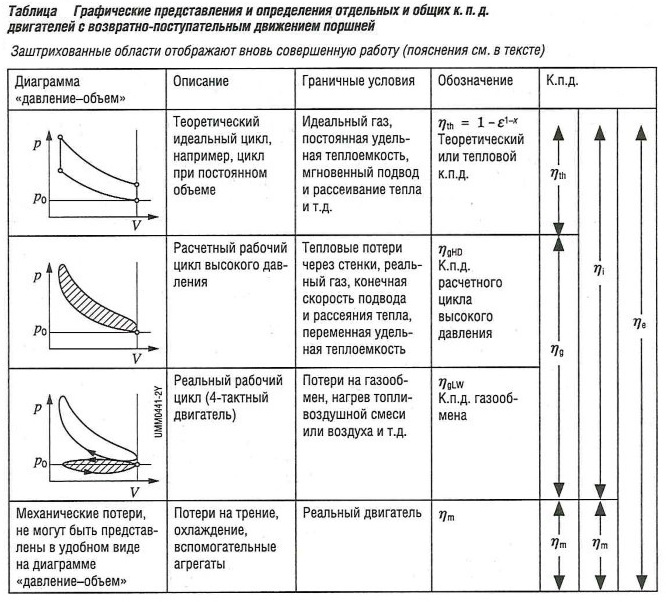
Фактор эффективности цикла описывает эффективность, с которой реальный цикл может быть аппроксимирован выбранным идеальным циклом. Поэтому он учитывает потери, в частности связанные с рассеива­нием. Для детального анализа потерь рекомендуется разделить фактор эффективности между петлей высокого давления и петлей цикла заряда (см. табл. «Графические представления и определения отдельных и общих КПД двигателей с возвратно-поступательным движением поршней»).

 

 

Обычно при расчете предполагается ра­бота с идеальным газом, с зависимыми от температуры теплоемкостями, и исполь­зуется идеальный цикл с геометрически идентичными размерами, таким же коэф­фициентом избытка воздуха, без остаточных отработавших газов, с полным сгоранием топлива и теплоизолированными стенками цилиндра. Описанный таким образом двига­тель также называется «совершенным дви­гателем». Значение фактора эффективности цикла при полной нагрузке составляет при­близительно 80-90%.

Если в расчете используется идеальный газ с постоянной теплоемкостью, можно ввести понятие «КПД совершенного двига­теля», который определяет мощность «иде­ального двигателя» относительно мощности «идеального цикла».

 

Коэффициент преобразования топлива

 

Бензиновые двигатели, работающие на бога­той топливовоздушной смеси (коэффициент избытка воздуха λ < 1) дают высокое содер­жание НС и СО в отработавших газах, что обычно не может быть учтено при рассмо­трении процесса подвода тепла через тепло­творную способность топлива H_UВ. Однако, экзотермичность этих газов Н_u является зна­чительной, что обычно проявляется в виде высоких температур отработавших газов на выходе из каталитического нейтрализатора отработавших газов окислительного типа. Это учитывается при помощи коэффициента преобразования топлива:

η_{B =} (H_UВ — Н_u) / H_UВ

Для дизельных двигателей обычно η_B = 1. Для бензиновых двигателей это значение мо­жет снижаться до 0,95, а при очень богатой смеси с λ < 1 становиться еще ниже.

 

Цепь КПД

 

Вся цепь к.п.д. может быть описана следую­щим образом (см. табл. «Графические представления и определения отдельных и общих КПД двигателей с возвратно-поступательным движением поршней» ):

η_eff = η₁ η_m = η_th η_g η_m

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: