Системы шасси автомобиля — это системы, состоящие из собранных воедино узлов ходовой части, трансмиссии и механизма управления. Системы шасси является одной из самых важных частей автомобиля и предназначена обеспечить восприятие и передачу всех сил, которые действуют на него во время движения.

 

 

 

Базовые принципы

 

Дороги, обычно используемые автомобилями, имеют неровности в диапазоне частот при­близительно до 30 Гц и являются наиболее интенсивным источником возбуждения в автомобиле. Возбуждения приводят к вер­тикальным перемещениям (вертикальному ускорению) автомобиля и пассажиров. Про­межуточным звеном между поверхностью до­роги и автомобилем является система шасси, главная задача которой — передача энергии между окружающей средой и кузовом. Это означает, что и на динамические характери­стики автомобиля, и на безопасность дорож­ного движения, а также на комфорт, сильно влияет выбор системы шасси.

Однако динамика реакции автомобиля опре­деляется не только компонентами системы шасси, она скорее является результатом со­четания различных общих параметров авто­мобиля. Как правило, повлиять на динамику автомобиля за счет работы над шасси оказы­вается весьма сложной задачей, в частности из-за того, что эффект изменений параметров должен преобладать среди конфликтующих приоритетов — безопасности движения и ком­фортабельности езды.

Безопасность движения в решающей мере зависит от контактных взаимодействий между шинами и поверхностью дороги, и стало быть от передаваемых продольных и поперечных сил. Поэтому фундаментальной целью при конфигурировании системы шасси в плане безопасности движения всегда является ми­нимизация динамический колебаний нагрузки на колёса, вызывающих снижение величину передаваемой силы.

С другой стороны, комфортабельность езды зависит от перемещений и ускорений, воздействующих на пассажиров (прежде всего, в вертикальном направлении). В за­висимости от области применения комфорт имеет большую важность и ни в коем случае не должен рассматриваться как сопутствую­щий элемент развития системы. В частности, в случае с профессиональными водителями, достаточно высокий уровень комфорта им не­обходим для предотвращения вреда здоровью. В этом контексте хорошим параметром оценки зарекомендовала себя эффективная величина ускорения кузова.

 

 

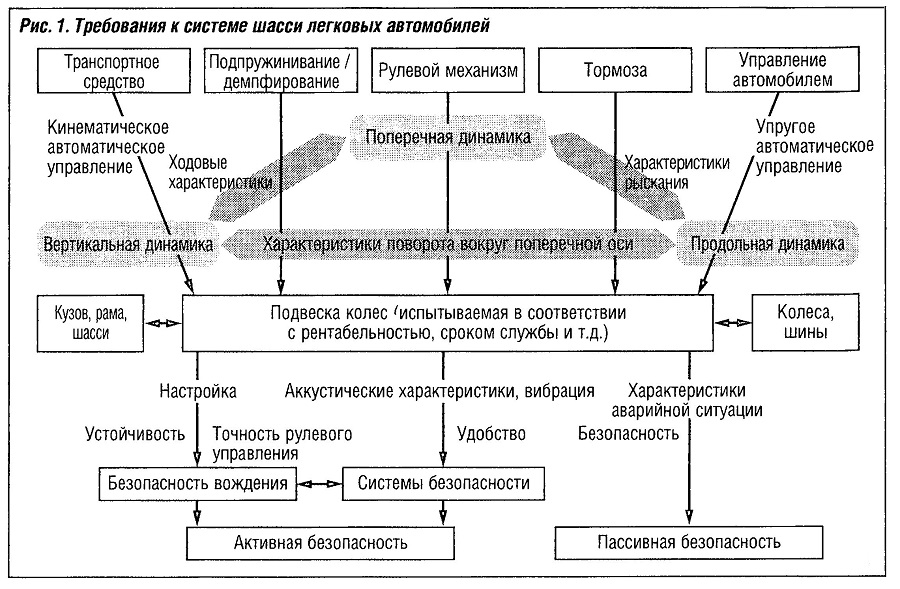
Однако эти ключевые параметры изначально лишь описывают потенциал системы шасси для соблюдения соответствующих требований. Фактическая динамика автомобиля, безопас­ность движения и комфорт также сильно зависят от выбора параметров дорожного покрытия (среды) и внутренних регулируе­мых переменных (например, угла поворота рулевого колеса или положения педали ак­селератора), задаваемых водителем. Фун­даментальные требования к системе шасси показаны на рис. «Требования к системе шасси легковых автомобилей». Шасси как система (без электроники) традиционно подразделяется на следующие подсистемы:

• Подвеска автомобиля;
• Амортизаторы;
• Подвеска колес и рычаги подвески;
• Шины;
• Рулевое управление;
• Тормозная система.

 

Возбуждение, вызываемое дорогой

 

Прежде, чем изложить основные принципы от­дельных компонентов «шасси» как системы, сначала обсудим понятие возбуждения, вы­зываемого дорогой, и затем — эффект возбуж­дения на вибрацию системы «автомобиль» в целом. Наряду с адаптацией системы колеба­ний к внешним возбуждениям, вызываемым дорогой, для автомобилей также требуется свести к минимуму влияние внутренних ис­точников возбуждения на характеристики вибрации (ДВС, колеса и шины).

Знание и описание в виде оптимизируе­мых параметров возбуждения, являющегося причиной вибраций, требуется для изучения характеристик вибрации и настройки системы подвески и амортизаторов в системе шасси. В то время как небольшие неровности можно скомпенсировать смягчающими характери­стиками шин, для уменьшения более значи­тельных перемещений кузова между кузовом и колесами необходим элемент, изменяющий свою длину. Здесь наиболее часто исполь­зуются стальные пружины, обеспечивающие возвращающую силу, зависящую от изменения длины. Результат — с учетом массы колес и кузова — система, способная вибрировать и требующая дополнительных элементов для гашения колебаний.

 

Виды неровностей

 

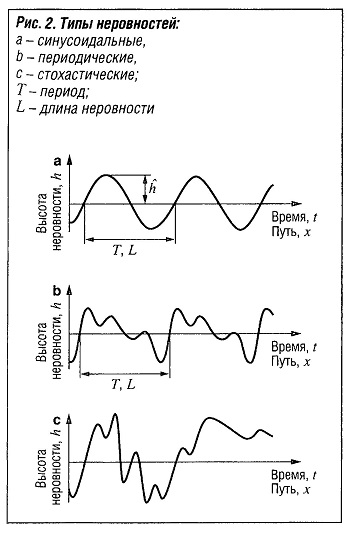Описывая неровности на дороге в зависимости от пути или времени, мы различаем гармони­ческие (синусоидальные), периодические и стохастические неровности (рис. «Типы неровностей»).

 

Гармонические неровности

 

В этом случае (рис. «Типы неровностей, а»), высота неровности h в зависимости от пройденного пути х или момента времени t будет равна:

h(x) = h sin(Ωx + ԑ) , а h(t) = h sin(ωt + ԑ)

где:

h- амплитуда;

L- длина неровности;

v- скорость;

ԑ- сдвиг фазы;

Ω = 2π/L — дорожная частота;

ω = vΩ = 2πv/L- угловая частота.

 

Периодические неровности

 

На следующем этапе предполагаются не только чисто синусоидальные, но также и периодические неровности (рис. «Типы неровностей, b»). Это означает, что выражение зависимости в виде ряда Фурье (периодические функции можно описать как бесконечный ряд синусоидальных колебаний) будет иметь вид:

h(х) = h₀ + Σ^∞_k-1 h_k sin(Ωx + ԑ_k)

h(t) = h₀ + Σ^∞_k-1 h_k sin(ωt + ԑ_k)

где:

h₀ — базовая амплитуда;

h_k— амплитуда;

ԑ_k — сдвиг фазы;

ω = 2π/L — дорожная частота;

L-длина неровности.

 

Стохастические участки неровности

 

Для поверхностей реальных дорог, т.е. не только для периодических, но и случайных (стохастических) неровностей (рис. с, «Типы неровностей» ), вы­сота неровности определяется через интеграл, соответственно перемещаясь из дискретного в непрерывный спектр:

h(x) = ∫^∞_-∞ h(Ω) e^jΩxdΩ

с непрерывным амплитудным спектром:

h(Ω) = 1/2π ∫^∞_-∞ h(x) e^-jΩxdx 

или в диапазоне времени:

h(t) = ∫^∞_-∞ h(ω) e^jΩtdω

где h(ω) = 1/v h(Ω)

 

Спектральная плотность мощности неровностей дороги

 

Но как правило, неровность в зависимости от пути или времени меньше подходит для теоретических исследований возбуждения, вызываемого дорогой. Значительно более интересным представляется знание средне­статистического возбуждения, возникающего при езде по определенному дорожному по­крытию, в частности, в сравнении с разными покрытиями. Вот почему для оценки возбуж­дения в основном используется спектральная плотность мощности Ф_h(Ω) в зависимости от дорожной частоты и спектральная плотность мощности в зависимости от угловой частоты Ф_h(ω). Математическое определение и под­робное обсуждение этих переменных я здесь не привожу. Для следующего исследования достаточно описательного значения спектральной плотности мощно­сти, существующей в «энергии в бесконечно малом диапазоне частот» (относительно пути или времени) или «выхода мощности в диа­пазоне собственной частоты».

Учитывая, что  L = vT, Ф_h(Ω) и Ф_h(ω) могут быть преобразованы друг в друга. Это можно описать уравнением:

Ф_h(ω) = 1/v Ф_h(Ω)

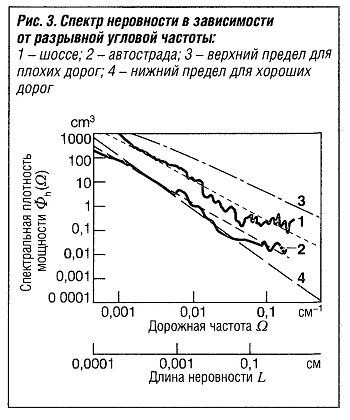Спектральная плотность мощности определяет распределение мощности спектра возбужде­ния по всему спектру неровностей. Обычно это представляют на двойной логарифмической шкале (рис. «Спектр неровности в зависимости от разрывной угловой частоты»). Приближение участков спек­тральной плотности мощности на реальных дорожных покрытиях возможно здесь с пря­мыми линиями, как это видно в следующем уравнении:

Ф_h(Ω) = Ф_h(Ω₀) (Ω/Ω₀)^-w  

где:

Ф_h(Ω₀) — спектральная плотность мощности с опорной угловой частотой Ω₀ (как правило, Ω₀ = 1 м^-1, что соответствует опорной длине волны неровности L₀ = 2π/Ω₀ = 6,28 м);

w — волнистость поверхности дороги (от 1,7 до 3,3; для стандартных дорог w = 2).

Если степень неровности и волнистость по­верхности дороги известны, то все параметры в приведенном выше линейном уравнении за­даны, и тогда его можно использовать для характеристики различных типов поверхности дороги. Степень неровности определяется как спектральная плотность мощности при опор­ной угловой частоте, т.е. Ф_h(Ω₀).

 

Основные принципы вибрационных характеристик автомобилей

 

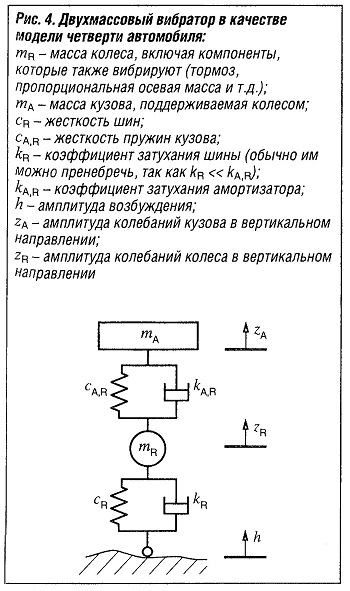Создаваемые дорогой возбуждения воздей­ствуют на кузов автомобиля через шины, подвеску колес и систему подвески / аморти­заторов. Для теоретического анализа можно использовать вибрационные модели различ­ной сложности. С ростом сложности модели повышается количество степеней свободы и связанных дифференциальных уравнений. Для большей ясности фундаментальные взаимосвязи в автомобильных вибрационных системах будут разъяснены на примере двух­массового вибратора (рис. «Двухмассовый вибратор в качестве четверти автомобиля»).

 

С указанием значений массы, коэффициен­тов упругости и коэффициентов затухания все параметры в двухмассовой модели для техни­ческого анализа вибраций заданы, и с пере­менными, обозначенными на рис. «Двухмассовый вибратор в качестве четверти автомобиля», можно составить два дифференциальных уравнения:

m_Az_A + к_А,R (z_A — z_R) + c_A,R (z_A — z_R) = О,

m_Rz_R — к_А,R (z_A — z_R) — c_A,R (z_A — z_R) + c_Rz_R + k_R z_R = c_Rh + k_Rh

Деление этих уравнений на массу в каждом случае приводит к обычному виду дифференциального уравнения 2-го порядка и дает угловую частоту свободных затухающих колебаний ω_g и угловую частоту свободных незатухающих колебаний ω_u, а также коэффи­циенты затухания для колеса D_R и кузова D_A.

Нижеследующее уравнение применимо к угловой частоте независимых незатухающих колебаний колеса:

ω_R=√ (c_R+c_A,R)/ m_R ≈ √ (c_R / m_R)_,при (c_R ≈ 10 c_A)

Нижеследующее уравнение применимо, соот­ветственно, к кузову:

ω_A=√ (c_A,R / m_A )

Вообще, угловая частота свободных затухаю­щих колебаний ω_g вычисляется по формуле:

ω_g = ω_{u√ (}1 — D²)

где в качестве приближения предполагается следующее: ω_g≈0,9 ω_u.

Нижеследующее уравнение применимо к ко­эффициенту затухания D_R на колесе:

D_R = к_А,R / 2m_R ω_{R =} к_А,R /2√(c_R+c_A,R)m_R = (m_Aω_A/m_R ω_R)D_A

где опыт показал, что нужно ориентироваться на D_R ≈ 0,4.

То же самое применимо к кузову:

D_A = к_А,R / 2m_A ω_A = к_А,R /2√(c_A,Rm_R)

В этом случае эффективность доказало зна­чение D_A≈ 0,3.

Колебания динамической нагрузки на колесо ΔG приводят к равенству:

ΔG = m_Rz_R + m_Az_A = c_R(h — z_R) + k_R (h — z_R)

Вместе эти переменные образуют основу для грубой конфигурации системы подвески / амортизаторов автомобиля.

Если известны собственная частота кузова (обычно f_А ≈ 1 Гц) и масса кузова (или удельная масса кузова на колесо), то можно определить жесткость пружин кузова относительно колес:

c_A,R = m_A ω_A²

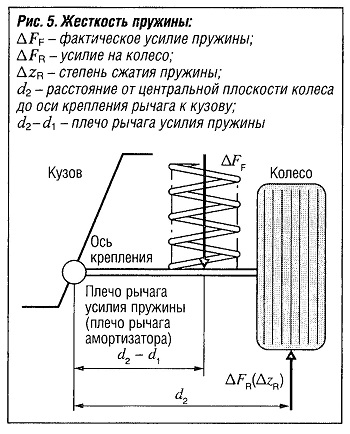Преобразование в фактическую жесткость пружин кузова имеет место с учетом соот­ношения i между перемещениями колеса и пружины, (см. рис. «Жесткость пружины»). Прежде всего, фактиче­ское усилие пружины

Δ F_F = с_А Δz_F 

и усилие колеса ΔF_R формулируются со сжа­тием пружины Δz_R . Нижеследующее уравне­ние применимо Δ F_R:

Δ F_R = c_A,R Δz_R 

Равновесие крутящего момента, действующего вокруг крепления рычага подвески к кузову оси, показанного на рис. «Жесткость пружины» приводит к:

c_A,R  Δz_R  d₂ = с_А Δz_F ( d₂ — d₁)

 

Это уравнение можно использовать для пре­образования фактической жесткости пружины с_А в соответствии с геометрическими взаимос­вязями с жесткостью колеса c_A,R:

c_A,R = с_А i²

с жесткостью пружины i:

i = ( d₂ — d₁)/d₂ = Δz_F /Δz_R

To же самое справедливо для гасителя ви­браций. Для расчета коэффициента затухания вибраций кузова (его эффект на колесо), в отношении колеса применимо следующее выражение:

c_A,R = 2D_A√(c_A,Rm_R)

 

При D_A = 0,3 (см. выше) и m_А, как известной переменной изучаемого автомобиля, коэф­фициент затухания вибраций кузова можно определить c помощью уравнения

D_R = (m_Aω_A/m_R ω_R)D_A

оценка оптимальных соотношений между мас­сами колеса и кузова с помощью коэффициен­тов затухания D_R = 0,4 и D_A = 0,3 (ориентиры) дает следующее соотношение:

m_A/m_R = 0,4ω_R / 0,3ω_A=0,4 f_R/0,3 f_A

 

где f_R= ω_R 2π и f_A= ω_A 2π.

При  f_R = 12 Гц  и  f_A = 1 Гц результат будет следующий:

m_R = 1/16 m_A

 

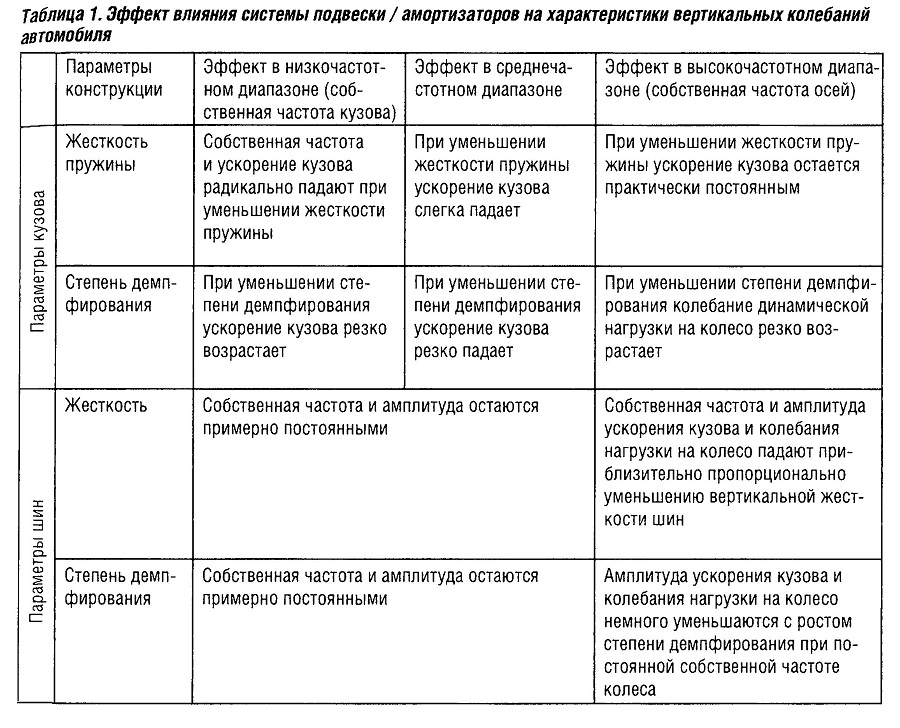
Влияние различных параметров подвески/амортизаторов на разные диапазоны частоты показано в таблице «Эффект влияния системы подвески / амортизаторов на характеристики вертикальных колебаний автомобиля».

 

 

Передаточная функция и спектральная плот­ность мощности ускорения кузова и колеба­ний нагрузки на колесо

 

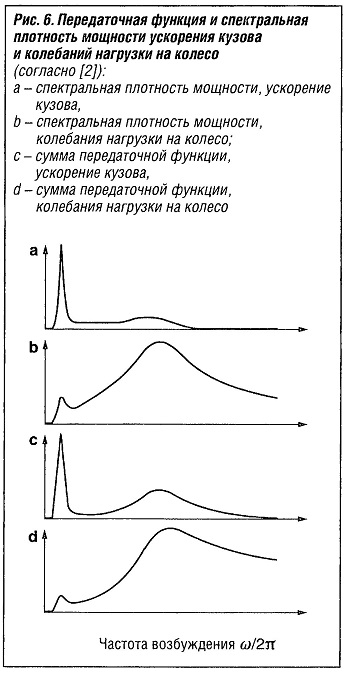Сумма передаточной функции — это отношение амплитуды выходных переменных (ускорения кузова или колебаний нагрузки на колесо) и амплитуды входной переменной (вертикальное возбуждение, см. рис. 4). Прин­цип прогрессии показан на рис. с и  d «Передаточная функция и спектральная плотность мощности ускорения кузова и колебаний нагрузки на колесо».

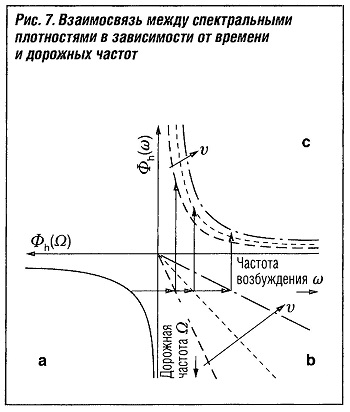
Теперь эти передаточные функции нужно привязать к неровностям дороги. Для этого предположим, что распределение неровно­стей дороги является функцией дорожной частоты (рис. а «Взаимосвязь между спектральными плотностями в зависимости от времени и дорожных частот»), и дорожная частота на основе скорости движения v (рис. 7b) преобразуется в угловую частоту, зависящую от времени (рис. 7с). На рис. 7с видно, что амплитуды возбуждения на низких частотах значительно больше, чем на высоких. Пере­даточные функции для ускорения кузова (рис. 6с) и колебаний нагрузки на колесо (рис. 6d) возводятся в квадрат и умножаются на этот спектр возбуждения. В результате получаем спектральную плотность мощности для уско­рения кузова (рис. 6а) и колебаний нагрузки на колесо (рис. 6b).

Более высокие амплитуды возбуждения поверхности дороги при низких частотах увеличивают амплитуду вибрации в диа­пазоне частоты собственных колебаний ку­зова (1-2 Гц). Однако в диапазоне частоты собственных колебаний колеса (10-14 Гц) низкие амплитуды неровностей приводят к падению спектральных плотностей мощности по сравнению с передаточными функциями, а это значит, что движения кузова становятся более доминирующими, чем движения осей.

 

Квантификация вибраций автомобиля

 

Почти сразу после появления автомобиля, в начале 20-го века были разработаны под­ходы к квантификации комфортабельности езды. Очень быстро было обнаружено влия­ние комфорта — в частности, в случае с профессиональными водителями — на хорошее физическое и психическое состояние, а также на здоровье водителя и, стало быть, на общую безопасность дорожного движения. Соответ­ственно, были предприняты попытки вывести переменные, описывающие комфорт, и срав­нить их в виде объективных коэффициентов комфорта для различных типов автомобилей и дорог. С тех пор был определен целый ряд различных методов оценки, основанных почти исключительно на сигналах ускорения в районе сиденья водителя и вокруг него. Здесь учитывается частотно-зависимая чувствитель­ность людей к вибрациям и колебаниям, возни­кающим в различных положениях, имеющим различный характер и направленность (по­ступательная или вращательная; направления х,у,z) посредством соответствующих взвеши­вающих частотных фильтров.

Широко используются два подхода-Дирек­тива VDI 2057 и стандарт ISO 2631. Эти методы анализа, несмотря на относительно низкие затраты по сравнению с другими, имеют большое информативное значение. В то же время, они образуют основу для многих других подходов к оценке комфорта, разра­ботанных в 90-е годы и позднее. В используемых до сих пор методах ускорения, вызываемые возбуждением в различных точках измерения (положениях инициации), обычно служат для определения коэффициента общего комфорта (например, на основе нескольких частичных коэффици­ентов комфорта в различных точках измере­ния), т.е. измерения нагрузки на пассажиров. Ускорения являются прежде всего частотно- взвешиваемыми (т.е. амплитуды различных частот привязаны к частотно-зависимым коэффициентам) и впоследствии приводятся к какому-то значению, например, по методу среднеквадратических значений RMS в соответствии со следующим уравнением:

a_RMS= √ (1/T ∫^T₀ a_w²(t) dt )

или по методу среднеквадратических значений RMQ (корень четвертой степени, в со­ответствии со следующим уравнением:

a_RMQ= ⁴√ (1/T ∫^T₀ a_w⁴(t) dt )

В зависимости от количества оцениваемых точек измерения в последующей операции должен формироваться общий коэффици­ент. Для Директивы VDI 2057 имеет отношение только оценка точки измерения с наибольшей нагрузкой. Все поступательные ускорения этого положения инициации (рука, сиденье или нога) в одинаковой мере учитываются в расчете коэффициента. Однако для взвешива­ния отдельных положений инициации пока не разработано никаких единых спецификаций. Причина этого кроется в том, что многие общие условия предметных испытаний определяли правило суммирования для общего коэффи­циента комфорта, образуемого из частичных коэффициентов комфорта, сильно отличавшихся друг от друга.

Для обеспечения сопоставимости коэффи­циентов отдельных методов расчета общий коэффициент комфорта часто стандартизиру­ется по стандартной шкале VDI. В то же время, объективным коэффициентам присваиваются вербализованные уровни интенсивности на­грузки (в помощь оценке предметов испы­таний).

Разница между отдельными методами оценки комфорта кро­ется в основном в количестве оцениваемых точек измерения, в спецификации расчета для образования частичного коэффициента комфорта из сигнала временного ускорения (метод RMS и RMQ) и, наконец, в рассеянном взвешивании различных сигналов ускорения при слиянии для образования общего коэффи­циента комфорта. К тому же еще окончательно не прояснён вопрос касательно частотного взвешивающего фильтра, используемого в зависимости от точки измерения. Функции взвешивания частоты, большинство из кото­рых определены эмпирическим путем, сильно отличаются друг от друга, особенно в низко­частотных диапазонах (ниже 1 Гц).

Эксперты также критикуют тот факт, что при группировании различных типов ускорения и направлений для образования отдельного коэффициента комфорта происходит потеря информации. Это означает, что при опреде­ленных обстоятельствах такие эффекты, как рост одного частичного коэффициента с одновременным уменьшением других частич­ных коэффициентов в одной и той же точке измерения (например, другого направления) и результирующее компенсаторное влияние на общий показатель комфорта останутся не выявленными. Этого можно избежать пу­тем оценки временных прогрессий частотно- оцениваемых ускорений непосредственно перед образованием частичного показателя комфорта.

 

Меры по минимизации вибрации

 

Создаваемые дорогой возбуждения приводят к вибрации осей и кузова автомобиля. Ее следует избегать путем минимизации колебаний дина­мической нагрузки на колесо (безопасность движения) и ускорений кузова (комфортабель­ность езды). Они уменьшаются с помощью соответствующих компонентов в подвеске колеса, при этом в зависимости от области применения свою эффективность доказали различные системы подвески, амортизации и рычагов.

Для решения этих задач традиционно ис­пользуются пружины и амортизаторы кузова. В сочетании с кинематикой и эластокинематикой в подвеске колес, настраиваемыми в соответствии с потребностями, они призваны обеспечить оптимальную передачу сил между шинами и дорожным покрытием и, одновре­менно, высокий уровень комфорта.

Однако с распространением актюаторов в системах шасси (например, рулевое управле­ние с наложением или векторизация крутящего момента) возрастает важность затрат на опти­мизацию подсистем. Одной из наиболее важ­ных причин этого является рост добавочной стоимости продукта из-за низкой стоимости интеграции функций со стороны программ­ного обеспечения (т.е. полной реализации различных функций различных подсистем в программной среде без необходимости увеличения технологических затрат). Кроме того, можно значительно увеличить технико­экономический синергетический потенциал в системе автомобиля в целом и улучшить по­тенциал дифференцирования различных про­изводных с помощью одних и тех же электрон­ных и программных модулей. Это означает, что электроника и программное обеспечение приобретают всё большую важность в области систем шасси, требуя междисциплинарного взаимодействия между аппаратной частью, электроникой и разработчиками ПО на очень ранних стадиях разработки для обеспечения эффективной и не затратной разработки мехатронных систем, особенно там, где безопасность движения является критичной.

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: