Метод конечных элементов – это метод приближенного численного решения физических задач. В его основе лежат две главные идеи: дискретизация исследуемого объекта на конечное множество элементов и кусочно-элементная аппроксимация исследуемых функций.

 

 

 

Применение метода конечных элементов

 

Практически все технические процессы могут быть смоделированы на компьютере при по­мощи метода конечных элементов — FEM (тер­мин был введен Реем У. Клафом в начале 1960-х годов). Этот метод подразумевает разбиение любого тела (газообразного, жидкого или твер­дого) на элементы простой формы (линия, треу­гольник, квадрат, тетраэдр, пентаэдр, гексаэдр), размеры которых являются минимально воз­можными, и которые постоянно связаны друг с другом в своих экстремальных точках («узлах»). Небольшие размеры элементов очень важны, поскольку поведение элементов, описываемое с помощью аппроксимации линейными уравне­ниями, применимо только к бесконечно малым элементам. Однако время, затрачиваемое на вычисления, требует применения метода конеч­ных элементов. Приближение к реальности тем лучше, чем меньше размеры элементов.

На практике применение метода FEM, также известного как FEA (анализ методом конечных элементов), началось в начале 1960-х годов в авиационной и аэрокосмической отраслях, но очень скоро метод нашел применение в автомобилестроении. Сегодня метод исполь­зуется во всех областях деятельности, включая прогнозирование погоды, медицину, и многие приложения автомобилестроения, от расчета компонентов двигателя и шасси до прогнози­рования поведения кузова при столкновении.

Имеются два различных способа при­менения FEM. Изначально использовался «черный ящик» FEM, который входил в со­став всех программ CAD (компьютеризован­ного проектирования) и предназначался для грубых расчетов, выполняемых инженером- конструктором (например, при конструиро­вании бампера), но затем применение метода было оставлено за специалистами по при­кладным программам FEM (например, пред­назначенным для расчета кузова, разработки мостов или расчета динамики движения).

 

Программное обеспечение FEM

 

В программное обеспечение FEM входят препро­цессор, постпроцессор и собственно программы FEM. Создание сети, т.е. разбиение на элементы, в основном, выполняется в препроцессоре на основе геометрии CAD, которая считывается непосредственно или через нейтральные ин­терфейсы, такие как IGES (исходный стандарт обмена графическими данными), VDA-FS (интер­фейс для технических характеристик элементов и точек, установленных союзом немецких автомобилестроителей) или STEP (стандарт по обмену данными моделей изделий). Программа FEM рас­считывает сформулированную таким образом модель вычислений. Полученный результат за­тем отображается в графической форме в пост­процессоре (например, распределение нагрузок в виде линий одного цвета, показ механических напряжений в форме анимации).

 

Основные сведения по применению метода конечных элементов

 

Подобно всем числовым методам, FEM пред­ставляет собой процесс аппроксимации. В механике, основной сфере применения FEM, ограничения, налагаемые на этот метод, описываются следующим образом.

 

Малые перемещения за один шаг решения

 

Тела движутся по траекториям, которые обычно являются кривыми высшего порядка. В соответ­ствии с основным принципом линеаризации, эти перемещения ограничиваются прямолинейными траекториями, которые могут быть описаны ли­нейными уравнениями. Будучи перенесенными к экстремальным точкам элементов (узлам), они также перемещаются по прямой линии. Таким образом, узлы способны правильно совершать только очень малые перемещения (узел повора­чивается менее чем на 3,5°). Фактическое движе­ние вдоль любой траектории или нелинейное по­ведение материала описывается, таким образом, линейными перемещениями, шаг за шагом, при большом количестве малых шагов.

 

Точность вычислений

 

Система линейных уравнений составляется и решается при ограниченной точности вы­числений, производимых компьютером. Обычно для сохраненного в памяти числа используются 8 байтов (= 64 бита) с точно­стью вычислений до 13 значащих цифр, т.е. только первые 13 цифр числа могут быть представлены точно. Четырнадцатая цифра и все последующие цифры в этом числе яв­ляются случайными числами. Таким образом, это исключает возможность каких-либо раз­личий по жесткости отдельных компонентов модели. Например, при расчете деформаций каркаса кузова необходимо при измерениях деформации кузова, заменить пружины мо­ста жесткими опорами.

 

Интерпретация результатов

 

Большая опасность заключается в том факте, что формальная модель вычислений, пра­вильно сформулированная в начале, может создать действительно выразительные цвет­ные изображения, однако демонстрируемые результаты могут концентрироваться вокруг факторов, заслоняющих реальность.

Проблемы, возникающие в результате вы­шеуказанных ограничений, должны, следова­тельно, быть идентифицированы и помечены программой вычислений, с тем чтобы менее опытный пользователь также мог легко по­лучать правильные результаты.

 

Области применения FEM

 

Физика, с точки зрения приложений в тех­нике, в общем случае подразделяется на пять разделов: механика со статикой и кинемати­кой (например, кузов, мосты); динамика и акустика (например, шум, создаваемый авто­мобилем); термодинамика (например, темпе­ратурный режим в двигателе); электричество и магнетизм (например, катушка зажигания и датчики); оптика (например, фары). Что касается метода FEM, всегда проводится раз­личие между:

• Линейными и нелинейными, статическими и динамическими проблемами с деформа­циями, как неизвестными величинами для вычисления механических напряжений и динамического анализа;
• Стационарными (вневременными) и не­стационарными (зависящими от времени) потенциальными проблемами (например, температура, звуковое давление, электри­ческий или магнитный потенциал) с потен­циалами в качестве неизвестных величин;
• Связями различных областей, например, для расчета температурного поля и ре­зультирующих деформаций, напряжений и усилий в линейной статике вовремя пу­ска двигателя.

 

Элементы FEM

 

Свойства элементов определяют наиболее важные рабочие характеристики программы FEM. Качество элемента выражается степе­нью выбранной функции математического описания. Проводится различие между эле­ментами с линейным и квадратным описа­нием, которые распознаются по срединным узлам (находящимся в серединах сторон). Таким образом, качество модели вычислений зависит не только от крупности используе­мой сетки, но также в значительной степени от функции описания.

При этом проводится различие между эле­ментами трех типов — линейными, оболочко­выми и объемными.

 

Линейные элементы

 

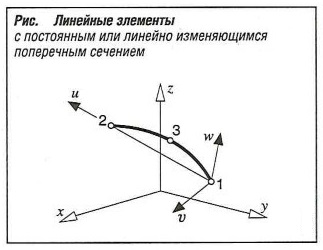Линейные элементы (рис. «Линейные элементы с постоянным и линейно изменяющимся поперечным сечением» ) являются пря­мыми или кривыми со срединным узлом. Поперечные сечения описываются посредством указания числовых значений площади поперечного сечения А , уменьшенных по­перечных сечений среза A_red-v-w (в областях среза), главных моментов инерции (I_V, I_W), крутящего момента инерции (I_t) с крутящим моментом сопротивления сечения (W_t), мо­мента инерции сектора при кручении, угла а, который описывает положение главных осей инерции v и w по отношению к плоскости дороги, и максимум четырех точек концен­трации напряжений (S_v, S_w) для вычисления напряжения изгиба.

 

Оболочковые элементы

 

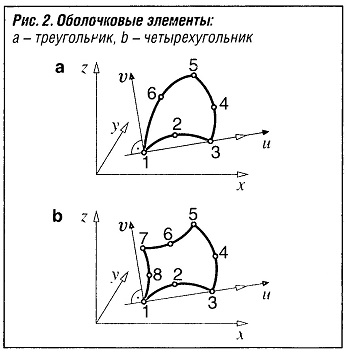Оболочковые элементы (рис. «Оболочковые элементы» ) по форме представляют собой треугольник или четы­рехугольник. В идеальном случае равносто­ронний четырехугольник или квадрат, обычно постоянной толщины. Если срединные узлы отсутствуют, края являются прямыми. Использования треугольников следует по воз­можности избегать или применять их только в переходных областях.

 

 

 

 

 

Объемные (сплошные) элементы

 

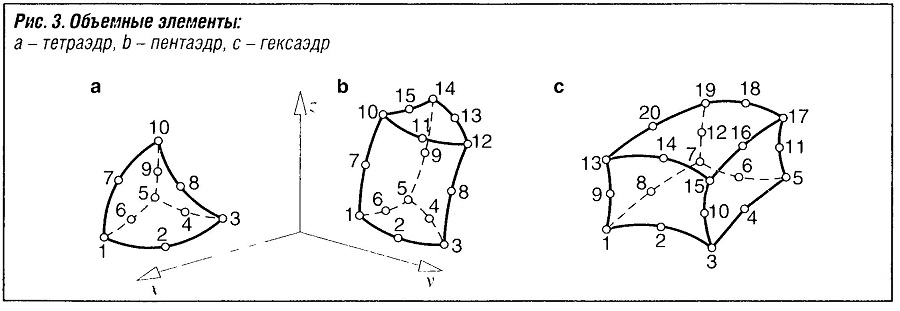
Объемные элементы (рис. «Объемные элементы» ) имеют форму тетраэдра, пентаэдра и гексаэдра, а в иде­альном случае — равностороннего тетраэдра или куба. При достаточном количестве эле­ментов по толщине (больше или равно трем) срединные элементы в настоящее время не используются. Однако, это не относится к тетраэдрам, которые почти всегда применя­ются в случае сложной геометрии деталей, таких как головка блока цилиндров.

 

 

Моделирование и оценка результатов

 

Наиболее важной функцией при использова­нии программы FEM является задача создания исходных данных в качестве модели вычисле­ний с использованием препроцессора. На эту задачу обычно уходит много времени. Поль­зователь должен стремиться достигнуть этой цели как можно меньшим количеством эле­ментов и узлов (однако, следует иметь в виду, что модель расчета, например, кузова может иметь примерно от трех до четырех миллионов узлов). Для этого пользователю следует обла­дать определенным опытом, а также он должен точно знать параметры используемых элемен­тов (см. ниже примеры FEM). Они могут не­сколько различаться в каждой программе FEM.

Первый шаг в процессе моделирования заключается в выборе типа элемента (линей­ного, оболочкового или объемного) и опреде­лении шага сетки, например, при помощи ука­занного расстояния от середины элемента до края. Следующий шаг заключается в опреде­лении свойств (данных материала), например, толщины элемента для оболочковых элемен­тов, значений площади поперечного сечения для линейных элементов и используемых единиц измерения (например, длина — в мм, усилие — в Н). Следующий шаг заключается в определении структуры опор и нагрузок. Решающим фактором в этом случае является рассмотрение точек, в которых модель зафик­сирована и нагружена. В отношении нагрузок также полезно выполнить разбиение общей нагрузки на расчетные, например, на нагрузку, вызванную силой тяжести, и нагрузки, возни­кающие во время движения.

Все результаты FEM доступны в форме перечня или в формате данных постпроцес­сора и, следовательно, могут быть показаны в виде графика (см. примеры FEM). В этом смысле постпроцессор предлагает все воз­можные формы отображения результатов.

 

Примеры FEM

 

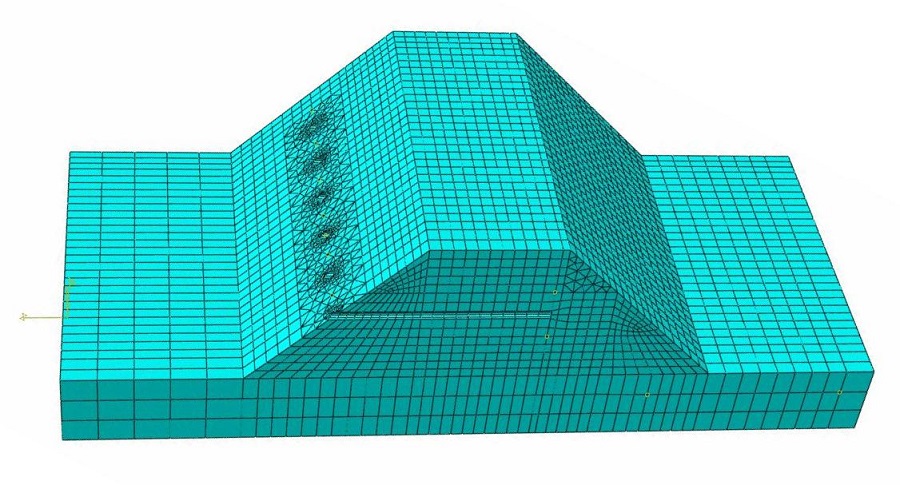
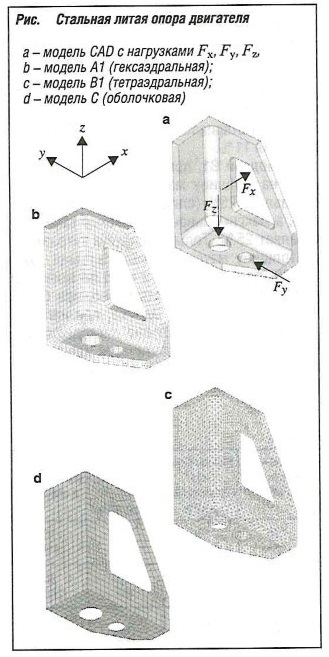В качестве примера приведем моделирова­ние, выполненное на основе геометрии CAD с использованием программы FEM ТР2000. Исходные данные для модели вместе с пред­ставлением результатов в цвете можно также найти на странице интернета.

В действительности все тела являются трех­мерными. При моделировании, для экономии времени и средств, часто выбирается упро­щенное решение. Например, намного легче вы­полнить автоматическое сеточное разбиение плоской поверхности в оболочковых элемен­тах, чем представлять тело в виде его объем­ных элементов. Часто используемая сетка те­траэдров, которую в настоящее время создает каждый препроцессор для любой объемной геометрии, не всегда оправдывает ожидания.

В автомобилестроении структурные ком­поненты являются либо толстостенными и сплошными (например, двигатель, транс­миссия, мосты, колеса) и моделируются при помощи объемных элементов, либо они из­готавливаются из тонкого листового металла (например, кузов автомобиля или кабина гру­зовика) и моделируются с использованием оболочковых и линейных элементов.

В первом примере модель на основе объем­ных элементов относится к первой группе тол­стостенных сплошных компонентов. Эта мо­дель сравнивается с моделью, используемой, в основном, на основе оболочковых элемен­тов, и принадлежащей ко второй группе. Эта модель также включает линейные элементы, часто применяемые в автомобилестроении, — они приведены во втором примере.

 

Пример 1: литая стальная опора двигателя как модель на основе оболочковых и объемных элементов (линейная статика)

 

Целью является сравнение оболочковых и объемных элементов в линейной статике на относительно толстостенной (3,75 мм) литой стальной опоре двигателя (50 x 25 x 57 мм³). Приведено сравнение двух моделей на основе объемных элементов А и В (каждая со сре­динными узлами и без них), результаты которых значительно различаются. В допол­нение к этому показана модель С на основе оболочковых элементов (рис. «Стальная литая опора двигателя» ). Начиная с объемной геометрии CAD препроцессор авто­матически создает сети объемных элементов А и В, а также модель С на основе оболочковых элементов при помощи модели поверхности.

Приняты следующие свойства материала:

• Модуль упругости (модуль Юнга) — 210 000 Н/мм²;
• Коэффициент Пуассона — 0,3;
• Плотность — 0,00000785 кг/мм³.

 

Для моделей А и В свойства элементов опреде­ляются типом элемента «сплошной» (объемный) с тремя степенями свободы узлов v_x, v_y и v_z. Для модели С свойства определяются типом элемента «пластина» (оболочковый элемент) с шестью степенями свободы узлов v_x, v_y, v_z, d_x, d_y, d_z и постоянной толщиной d= 3,75 мм.

В модели А сеточное разбиение на объ­емные элементы (сплошная сетка) демон­стрирует предпочтительное разбиение на гексаэдры (полностью автоматический про­цесс возможен не для любой геометрии, поскольку здесь, например, геометрическая форма сначала должна быть разбита на ба­зовые тела), а на модели В — автоматическое разбиение на тетраэдры. Указано также ко­личество элементов относительно толщины, что определяет точность (в этом случае, как минимум, используются три элемента).

 

Условия опор

 

На прямоугольной плоскости xz равенство v_y = 0 относится ко всем узлам. Все краевые узлы на правой, длинной стойке зафикси­рованы при v_x = 0, а узлы нижней, короткой стойки — при v_z = 0.

Нагрузки

 

∑F_X= 900 Н, ∑F_y =2006 Н, ∑F_Z =-550 Н.

 

Все нагрузки определены как поверхностные («на поверхности», для оболочковых эле­ментов — «на кривой») около углубления при F_λ = 600 Н, у малого отверстия-при F_y=2006 Н и у большого отверстия — при F_z = -550 Н.

Примечание: применение «изолирован­ных» отдельных нагрузок допускается только при использовании линейных элементов.

 

Результат

 

 

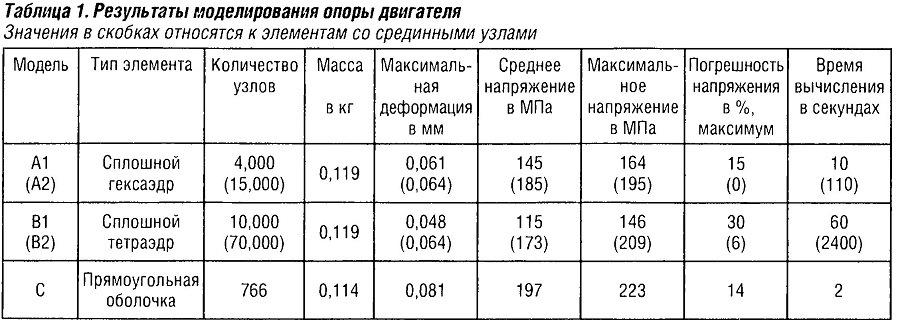
Результаты моделирования опоры двигателя приведены в табл. «Результаты моделирования опоры двигателя». На рис. «Распределение деформаций и напряжений в модели А2, взятой как корректная модель» показаны результаты для модели А. Напря­жения отображаются оттенками серого цвета (критические области затемнены) или, в ори­гинале, как области одинакового цвета.

Объемные элементы очень чувствительны к неправильно апроксимированным распре­делениям нагрузок. Следовательно, объем­ные элементы должны всегда испытывать только поверхностные нагрузки.

Детальное рассмотрение табл. «Результаты моделирования опоры двигателя»: правиль­ные результаты дает модель А2 с узлами в се­рединах сторон (v = 0,064 мм, σ = 195 МПа). Отклонение между средним и максималь­ным напряжениями в узле (со стороны всех элементов, примыкающих к одному узлу) должно быть как можно меньшим (менее 15%). На модели А1, при трех элементах на толщину материала, достигнуто значение от­клонения 11 %.

На модели В1, при наличии трех тетраэ­дров на толщину материала, деформация составляет 25% (слишком мала) (v = 0,048 мм), а максимальное напряжение также со­ставляет 25%. Только при двух тетраэдрах на толщину материала модель была даже на 58% более жесткой, и вряд ли могла бы использоваться, соответственно, при более низких напряжениях. Однако, при наличии срединных узлов (В2) она дает деформа­ции и напряжения, практически идентичные модели А2 с очень большим количеством узлов и большой продолжительностью вычислений. Следовательно, рекомендуется соблюдать осторожность при использовании тетраэдральных сеток без срединных узлов. Модель С с оболочковыми элементами без де­формации сдвига (предназначенная только для тонкостенных структур) является слишком мяг­кой (v = 0,081 мм, на 21 % больше, в то время как для толстостенных компонентов с учетом деформации сдвига это значение еще больше — на 30%). Оболочковые элементы, тонкостенные или толстостенные, дают значения деформа­ций, которые могут быть использованы только частично, при относительно большой толщине, в особенности в случае очень компактных тел, что имеет место и в данном примере. Однако при напряжениях +14% их использование по большей части безопасно.

 

Пример 2: трубчатый каркас кузова

 

Целью является выполнение анализа ме­тодом конечных элементов кузова в виде объемного каркаса без листовой обшивки, включая оптимизацию веса и жесткости, на примере мини-пикапа (не реальный автомо­биль).

Свойства материала:

• Модуль упругости (модуль Юнга) — 200 000 Н/мм²;
• Коэффициент Пуассона — 0,3;
• Плотность — 0,00000785 кг/мм³.

 

В целях упрощения в качестве профильных секций используются только две формы (см. рис. «Профильные секции объемного каркаса» ). Секция из профиля коробчатого сече­ния (90 х 120 х 1,5 мм³) и секция трубчатого профиля (70 х 2 мм²), которые определены в препроцессоре со своей формой непосред­ственно как элементы типа «стержень») с по­стоянным поперечным сечением (элементы с различными начальным и конечным сече­ниями определялись бы как «балка»). Это дает следующие требуемые значения сечения (в м², мм⁴ и мм³).

 

Коробчатый/трубчатый профиль:

 

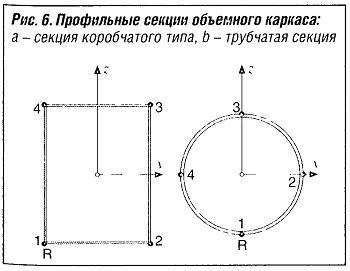
• Площадь поперечного сечения: А = 621/427;
• Уменьшенные поперечные сечения (в об­ласти сдвига): A_redl = 325/227; A_redll = 219/227;
• Главные моменты инерции: I_I = 1 348 306/247 168; I_II = 869 596/247 168;
• Момент инерции при кручении: I_t = 1 606 083/494 261;
• Крутящий момент сопротивления сечения: W_t = 7334/2177;
• Расположение главных осей инерции по отношению к дороге: a = 0°;
• Максимум четыре точки концентрации напряжений:

S_x = —45/45/45/—45 / 0/35/0/-35;

S_y = -60/-60/60/60 / -35/0/35/0.

 

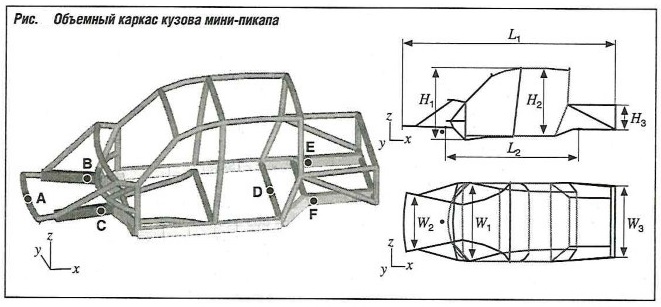
Основные размеры в мм в соответствии с видами сбоку и сверху (рис.  «Объемный каркас кузова мини-пикапа» ):

• L₁= 4 114 (максимум);
• L₂ = 2 650;
• W₁ = 1 517 (максимум);
• W₂ = 1 147 (спереди);
• W₃ = 1 374 (сзади);
• Н₁ = 1 402 (макс.);
• Н₂ =1 315;
• H_з = 469 (коробчатый профиль).

 

 

Конструкция

 

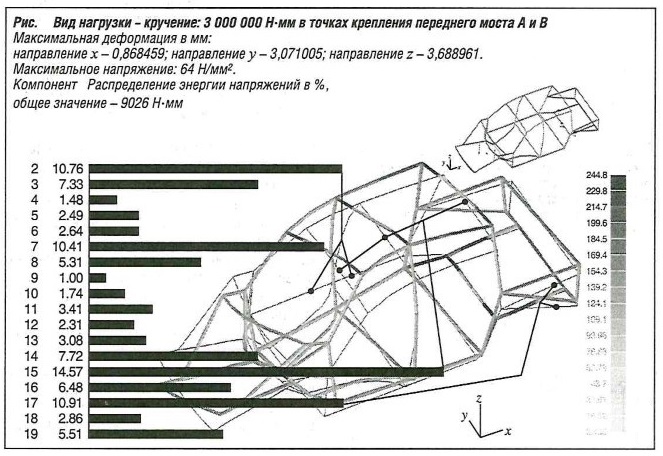
Объемный каркас состоит из 18 компонентов (рис. «Вид нагрузки-кручение» ):

• 2  — боковая стойка;
• 3 — поперечная опора педалей;
• 7 — поперечная опора кабины;
• 8 — передняя боковая стойка;
• 10-передняя вспомогательная попереч­ная стойка;
• 14 — боковой каркас крыши;
• 15 — поперечный каркас крыши;
• 16-задний подрамник;
• 17 — боковая стойка коробчатого сечения;
• 19 — задний бампер.

 

 

Условия опор:

 

Линейная статика, гид нагрузки — изгиб (не показан):

• A-v_y = 0; (A…F, см. рис. 7);
• В, С, Е, F — v_z = 0; D — v_x = 0, v_y = 0

 

Линейная статика, вид нагрузки — кручение:

• А, В, С — свободные;
• Е, F-vz = 0;
• D — v_x= 0, v_y = 0, d_y = 0, d_z = 0.

 

Степени свободы/динамика в свободном со­стоянии: без опор, кузов свободно вибрирует на пру­жинах.

 

Напряжения

 

Линейная статика, вид нагрузки — кручение: крутящий момент — 3 000 000 Н⋅ мм, при нор­мальной удельной нагрузке на опоры переднего моста В: F = -3 593,7 Н;

опоры переднего моста С: F = 3 593,7 Н.

Степени свободы/динамика в свободном со­стоянии: только массы, на которые действует сила тя­жести 170 кг, без дополнительных масс.

 

Результаты

 

Степени свободы/динамика в свободном со­стоянии:

• Кузов может свободно вибрировать на своих пружинах, значения собственных ча­стот недемпфированной, упругой системы в восходящем порядке; для свободных колебаний, начиная с нескольких типов колебаний (в данном случае — от 1 до 6) с собственной частотой 0 в каждом случае.
• Первая собственная частота (38 Гц) как частота первых крутильных колебаний, третья собственная частота (48 Гц) как частота первых изгибных колебаний; с нормализованными деформациями в каждом случае х, у, z во всех узлах (в дан­ном случае деформации нормализованы максимум до 0,1 мм), нормализованными напряжениями во всех элементах, и энергия напряжений, являющаяся важным па­раметром для оптимизации веса на один элемент и один компонент, от 1 до 18 % в виде гистограммы (как показано для случая линейной статики на рис. «Вид нагрузки-кручение» ). Абсо­лютные величины были получены только в случае расчета возбуждения.

 

Линейная статика:

 

• Деформации х, у, z во всех узлах;
• Силы и моменты реакции, действующие на все элементы, энергия напряжений, при­ходящаяся на элемент и компонент в %.

 

Оптимизация веса и жесткости

 

Формула вычислений для оптимизации веса и жесткости известна, начиная с 1960-х годов (максимальная погрешность для двойной жесткости -10 %). Изменение жесткости всей конструкции (в %) получено посредством умножения изменения жесткости компонента на долю энергии напряжений для компонента и деления результата на 100.

Эта формула используется специально в целях оптимизации практически во всех критичных для автомобиля случаях нагрузки при кручении с учетом других видов нагрузки. Таким образом, конструкция может быть усилена при помощи стоек, воспринимающих основную часть нагрузки, а вес может быть снижен за счет стоек, воспринимающих меньшую часть нагрузки.

 

Применение формулы

 

Первый компонент (см. рис. «Вид нагрузки-кручение» ): компонент 15 (каркас крыши, поперечный, G =11,85 кг с долей энергии напряже­ний 14,57%) дает изменение (уменьше­ние) момента кручения между мостами (14,57 х 116) /100 = 16,9 %, когда жесткость (момент инерции относительно плоскости) этого компонента увеличивается в 2,169 раза (на 116,9 %). В этом случае при увеличении диаметра трубы с 70 до 90 мм возрастание массы составляет 3,55 кг.

Второй компонент (см. рис. 8): компонент 6 (линейный усилитель­ный элемент, G = 11,14 кг с долей энер­гии напряжений 2,64%) дает изменение (2,64 х 250)/100 = 6,6 % (т.е. очень неболь­шое снижение момента кручения между мостами, когда жесткость (момент инерции) этого компонента уменьшается в 3,5 раза (на 250%). В этом случае при уменьшении диа­метра трубы с 70 до 50 мм снижение массы составляет 3,34 кг.

 

Результат

 

Минимальное увеличение массы на 3,55 — 3,34 = 0,21 кг дает увеличение жесткости при кручении на 16,9 — 6,6 = 10,3% (проверка при измененных профильных секциях дает зна­чение 9%; это объясняется малым значением погрешности формулы вычислений).

Диаграммы распределения энергии напря­жений для других случаев нагрузки (здесь не показаны) показывают, что это также относится к крутильным колебаниям и не имеет значения для изгиба. Таким образом, можно значительно повысить для этого ку­зова жесткость при кручении и жесткость на изгиб и безопасно снизить общую массу посредством уменьшения поперечных се­чений компонентов, имеющих избыточные размеры.

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: