Математика, это наука о количественных отношениях и пространственных формах действительного мира; греческое слово (математикэ) происходит от греческого же слова (матема), означающего «знание», «наука». Математика возникла в глубокой древности из практических потребностей людей и её связи с практикой со временем становились все более и более многообразными, и глубокими. Содержание и характер математики изменялись на протяжении всей истории и продолжают изменяться в настоящее время. Вот о том, какова сегодня автомобильная математика, мы и поговорим в этой статье.

 

 

Системы чисел

 

Физические и технические величины описываются их числовыми значениями и единицами измерения. Числа обычно представляются в десятичной системе счисления, т.е. системе с основанием 10. Другими распространенными системами счисления являются двоичная и шестнадцатиричная системы с основанием, соответственно, 2 и 16.

В то время как в десятичной системе используются цифры 0,1-9, в двоичной системе используются только цифры 0 и 1. В шестнадцатиричной системе в дополнение к цифрам 0,1 -9 используются буквы A, B-F, представляющие числа 10,11-15 (см. таб. «Преобразование десятичных чисел в двоичные» и табл. «Преобразование десятичных чисел в шестнадцатиричные» ).

Двоичная и шестнадцатиричная системы счисления используются в основном в информационных технологиях, поскольку компьютер может обрабатывать информацию только с помощью двух символов — «0» и «1». Эти два символа и составляют основу двоичной системы. Когда восемь двоичных цифр объединяются в один байт, появляется возможность представлять десятичные числа 0-255, что соответствует шестнадцатиричным числам 0-FF.

 

 

Функции

 

Функция в математике, это соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества. Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины.

 

Экспоненциальная функция

 

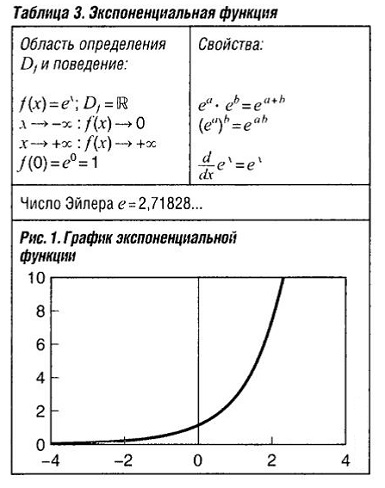
Экспоненциальная функция описывает процессы, где прирост пропорционален количеству, например, у логарифма числа есть, по определению, степень, в которую должно быть возведено основание, чтобы дать число, от которого берется логарифм ln y = x. Если это определение применить к числу, которое равно e^x(y = e^x), то: ln e^x = x 

Поскольку e постоянная, e^x зависит от числа x.  Мы таким образом говорим, что e^x есть функция x. К тому же, поскольку x есть показатель степени e, то e^x известна как экспоненциальная функция. (см. табл. «Экпоненциальная функция» )

 

Логарифмическая функция

 

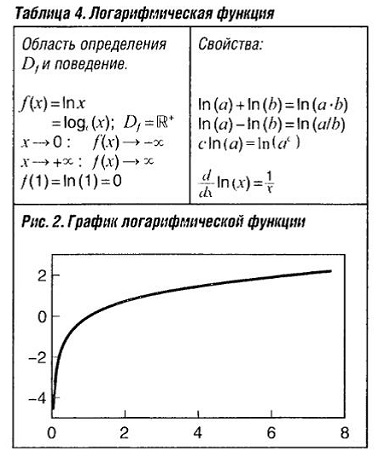
Логарифмическая функция является одной из основных элементарных функций. Функцию вида    y = log_a(x), где a любое положительное число не равное единице, называют логарифмической функцией с основаниема. Она представляет собой функцию, обратную экспоненциальной функции. (см. табл. «Логорифмическая функция» )

 

 

 

Тригонометрические функции

 

Тригонометрические функции, это элементарные функции, которые возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге. Эти функции нашли широчайшее применение в самых разных областях науки. Тригонометрические функции любого угла можно свести к тригонометрическим функциям острого угла, используя их периодичность и так называемые формулы приведения. Это необходимо, например, для нахождения значений тригонометрических функций по таблицам, поскольку в таблицах обычно приводятся значения только для острых углов.

 

Синус и косинус

 

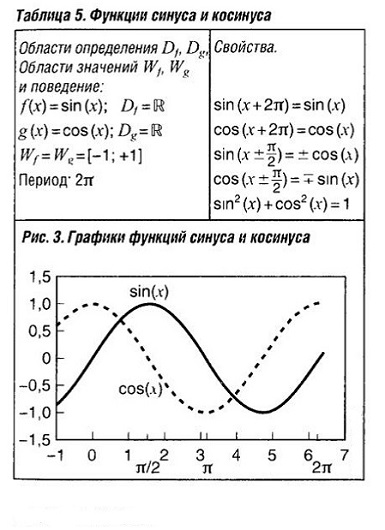
Синус, это одна из тригонометрических функций и обозначается sin. Синусом ​угла в треугольнике называют отношение катета, лежащего против этого ​угла (противолежащего катета) к гипотенузе. Косинус, это одна из тригонометрических функций, обозначается cos. ​Косинусом угла в треугольнике называют отношение катета, лежащего ​рядом с этим углом (прилежащего катета) к гипотенузе. (см. табл. «Функции синуса и косинуса» )

 

Тангенс и котангенс

 

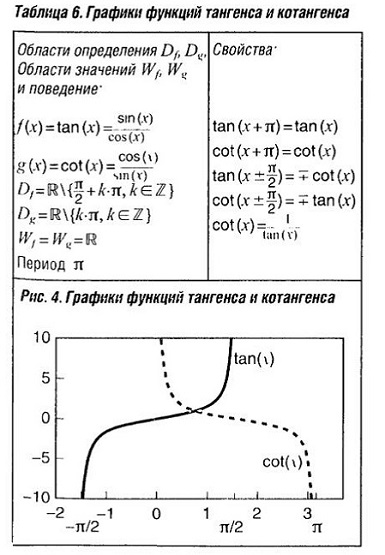
Тангенс, это отношение синуса к косинусу tg = sin/cos или отношение противолежащего катета к прилежащему. Котангенс, это отношение косинуса к синусу ctg = cos/sin или отношение прилежащего катета к противолежащему. (см. табл. «Графики функций тангенса и котангенса» )

 

Многочлены

 

Многочленом называется алгебраическая сумма нескольких одночленов. Одночлены, из которых составлен многочлен, называют членами многочлена. Многочлен степени n состоит из (n+1) слагаемых с действительными (или комплексными) коэффициентами a₀, a₁…, a_n и ассоциированными одночленами х:

f(x) = a₀ + a₁x + a₂x₂ + …+ a_nx_n

Многочлен степени n может иметь максимум n нулевых точек и (n -1) локальных экстремумов.

На рис. «Пример линии и параболы с двумя нулевыми точками» в качестве примера показаны прямая линия (многочлен первой степени) и парабола (многочлен второй степени).

 

Прямая линия

 

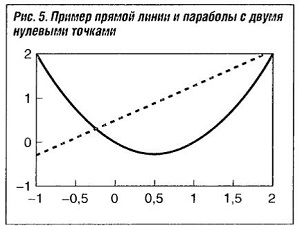Прямая линия является многочленом первой степени:

f(x) = a₀ + a₁x или y=mx+t  (с градиентом m и отрезком t, отсекаемым на оси ординат). Нулевая точка лежит на х₀=-t/m .

 

Парабола (квадратичная функция)

 

Парабола представляет собой многочлен 2-ой степени:

f(x) = a₀ + a₁x + а₂х² или у = ах² + bх + с.

Нулевые точки лежат на

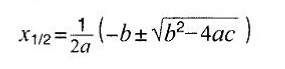
(решение квадратного уравнения).

Парабола может не иметь ни одной нулевой точки, либо иметь одну или две нулевые точки.

 

Функция квадратного корня

 

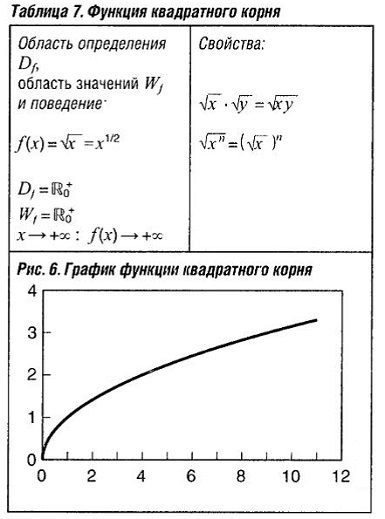Функция квадратный корень из x, например, y = √x является одним из частных случаев степенной функции. Эта функция не имеет своего собственного имени (в отличие от квадратичной функции или кубической функции) и называется просто формулой. График функции y равен корню из x — ветвь параболы. Функция квадратного корня представляет собой функцию, обратную квадратичной функции.

Аналогично, для каждого одночлена f(х)=хⁿ, n∈ N существует монотонно возрастающая обратная функция f^—1(x)=ⁿ√x=x^1/n, которая определена только для x ⩾0.

 

Абсолютная величина и знаковая функция

 

Каждое действительное число х может быть разбито на его знак и абсолютную величину I x l. При этом применимо следующее выражение: x=sgn(x)·|х|. Например, sgn(-3) = -1, a sgn(+4) = +1. Абсолютная величина выражает отклонение числа х от точки начала координат 0. Таким образом, функция абсолютной величины может быть представлена как:

 

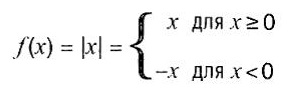
с областью определения D₁=R и областью значений W₁ = R₀⁺. При этом f(х) —> + ∞ для X —> ±∞.

 

Уравнения для плоского треугольника

 

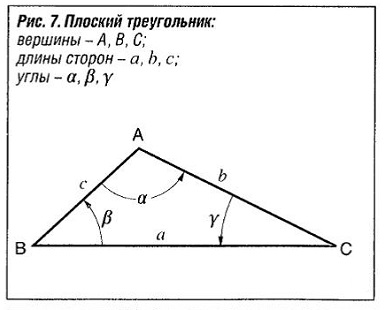На рис. «Плоский треугольник» показан плоский треугольник со сторонами a, b и с и углами α, β и γ. Соотношения между этими величинами описываются следующими уравнениями.

Сумма углов: α + β + γ = 180°.

Теорема синусов: a : b : с = sinα : sinβ : siny.

Теорема Пифагора: c² = a² + b²-2a· b·соsу (общая), с² = а² + b² (для прямоугольного треугольника).

 

 

 

Комплексные числа

 

Для комплексных чисел определены операции сложения, вычитания, умножения и деления. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел, например, два комплексных числа нельзя сравнивать на больше/меньше. Комплексное число z имеет действительную и мнимую составляющие. Мнимая составляющая умножена для z на мнимую единицу i. При помощи координат, а и b, можно представить число z в декартовой системе координат.

Комплексное число z в декартовой системе координат: z=a+i·b где i²=-1, действительная составляющая; а = Re{z},

мнимая составляющая b = lm{z}.

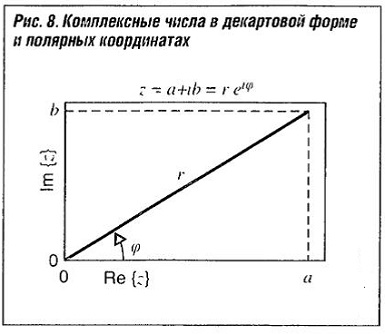
Декартова форма может быть при помощи простого преобразования переведена в полярные координаты r и φ (отклонение от начала координат и угол к оси х) (см. рис. «Комплексные числа в декартовой форме и полярных координатах» ).

Комплексное число z в полярных координатах.

z = re^iφ, где r=√a²+b² и tanφ=b/a, или a=r·cosφ и b=r·sinφ.

Комплексная экспоненциальная функция: e^tφ= cosφ + isinφ.

Правила вычисления:

В отношении комплексных чисел действуют те же правила вычисления, что и в отношении действительных чисел. При этом сложение легче выполнять в декартовых координатах, а умножение в полярных. Сложение: z₁ +z₂ = (a₁+a₂) + i (b₁ + b₂). Умножение: z₁·z₂ = (r₁·r₂) e ^{i (φ1 + φ2)}.

         Математические знаки и символы:                                   Греческий алфавит:

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: