Колебания, это многократное повторение одинаковых или почти одинаковых процессов. Сопутствуют многим природным процессам и явлениям, вызванным человеческой деятельностью — от простейших колебаний маятника до электромагнитных колебаний распространяющейся световой волны. Механические колебания — это периодически повторяющиеся движения, вращательные или возвратно поступательные. Это тепловые колебания атомов, биение сердца, колебания земли (моста) под ногами. В этой статье мы рассмотрим механические колебания и вибрации.

 

 

 

Определения

 

(Обозначения и единицы измерения в Табл. «Условные обозначения величин и единицы измерения», см. также DIN 1311).

 

Колебания или вибрации

 

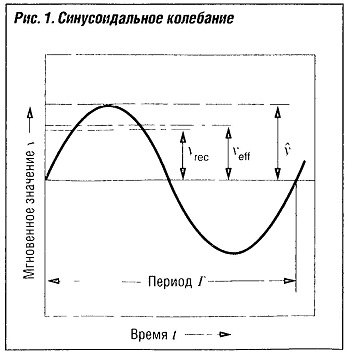Термины, применяемые для обозначения изме­нений какой-либо физической величины, более или менее регулярно повторяющихся во вре­мени и меняющихся по направлению (рис. «Синусоидальные колебания» ).

 

Период

 

Время Т, за которое совершается одно пол­ное колебание.

 

Амплитуда

 

Максимальное мгновенное (пиковое) значе­ние у, которого достигает какая-то физиче­ская величина, совершающая синусоидаль­ное колебание.

 

Частота

 

Число f колебаний, совершаемых в секунду. Это величина, обратная периоду колебаний Т.

 

Угловая частота

 

Угловая частота ω — это частота f умножен­ная на 2π.

 

Колебательная скорость частицы

 

Мгновенное значение переменной скоро­сти частицы v, движущейся в направлении колебания. Не следует путать со скоростью распространения бегущей волны (например, скоростью звука).

 

Ряды Фурье

 

Любую периодическую функцию, являющу­юся гладкой и кусочно-непрерывной, можно представить как совокупность синусоидаль­ных гармонических компонентов.

 

Биения

 

Биения происходят при наложении двух си­нусоидальных колебаний со схожей часто­той (f₁≈f₂). Они являются периодическими. Основная частота в этом случае равна раз­нице между частотами наложенных синусои­дальных колебаний.

 

Собственная частота

 

Собственная частота — это такая частота f при которой колебательная система коле­блется свободно после однократного возбуждения (собственные колебания). Она зависит только от характеристик самой колебатель­ной системы.

 

Демпфирование

 

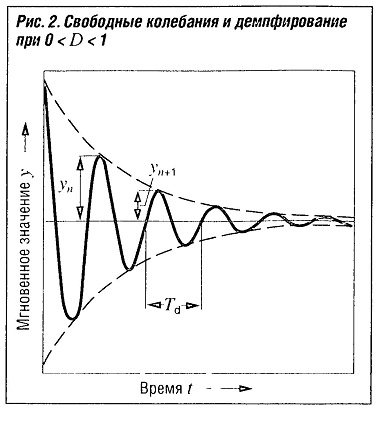
Мера потерь энергии в колебательной си­стеме при превращении одной формы энер­гии в другую. Следствием является затухание колебаний (рис. «Свободные колебания и демпфирование» ).

 

Декремент

 

Декремент D — это мера измерения степени демпфирования.

 

Логарифмический декремент

 

Логарифмический декремент Λ — это нату­ральный логарифм отношения двух экстре­мальных значений собственных затухающих колебаний, различающихся на один период.

 

Вынужденные колебания

 

Возникают под влиянием внешней физиче­ской силы (возбуждения). Частота вынуж­денных колебаний определяется частотой возбуждения.

 

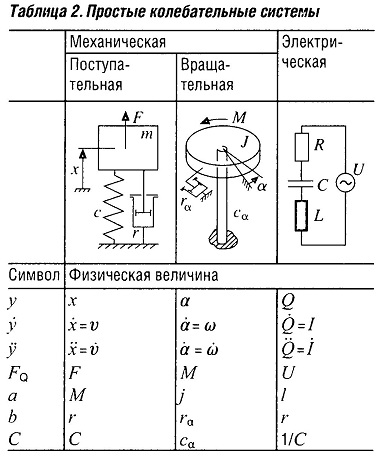
Передаточная функция

 

Передаточная функция — это частное ампли­туды наблюдаемого состояния или выходной переменной и амплитуды возбуждения, на­ходящееся в зависимости от частоты возбуждения f или частоты цепи возбуждения ω.

 

Резонанс

 

Возникает, когда передаточная функция при­нимает очень большие значения, при этом частота возбудителя приближается к соб­ственной частоте.

 

Резонансная частота

 

Частота резонатора, при которой колеблю­щаяся величина достигает своего макси­мального значения. Если пренебречь демп­фированием, резонансная частота равна собственной частоте.

 

Ширина резонансного пика половинной энергии

 

Разница между частотами, при которой уровень переменной величины падает до 1/ √ 2 ≈ 0,707 максимального значения.

 

Острота резонанса

 

Острота резонанса Q (или добротность) — это максимальное значение передаточной функции.

 

Соединение колебательных систем

 

Если две колебательные системы соединя­ются механически, посредством массы или упругости, либо электрически, посредством индуктивности или емкости, между ними происходит периодический обмен энергией.

 

Волна

 

Волна-это пространственное и временное изменение состояния среды, которое можно представить как однонаправленное ее пере­мещение. Если материя может существовать в пространстве, не обязательно, что она мо­жет быть перемещена.

Существуют поперечные и продольные волны.

 

Интерференция

 

Принцип независимого наложения волн. В любой точке пространства мгновенное зна­чение результирующей волны равно сумме мгновенных значений каждой из волн.

 

Плоская волна

 

Плоская волна — это волна, у которой по­верхности одинаковой фазы (например, максимумы или фронты волны) формируют плоскость, т.е. которая распространяется по линейному закону. Фронты волны располо­жены вертикально по отношению к направ­лению распространения.

 

Стоячие волны

 

Стоячие волны возникают в результате ин­терференции между двумя волнами, движу­щимися в противоположных направлениях, с равными длиной, частотой и амплитудой. Амплитуда стоячей волны постоянна в любой точке; узлы колебаний (нулевая амплитуда) и пучности (максимальная амплитуда) со­впадают. Стоячие волны наблюдаются, на­пример, когда плоская волна отражается от плоской поверхности, расположенной верти­кально по отношению к направлению распро­странения волны.

 

Значение выпрямления

 

Значение выпрямления у_rес — это среднее арифметическое значение, линейное во вре­мени, параметров периодического сигнала:

у_{rес = 1/T ∫|у| dt}

Для синусоидальной кривой:

у_{rес = 2} у/π ≈  0,637 у

 

Эффективное значение

 

Эффективное значение у_eff  это временное виртуальное значение периодического сиг­нала. Оно также известно как среднеквадра­тическое значение:

у_eff = √ (1/T ∫ у² dt)

Для синусоидальной кривой:

у_eff = у/√ 2 ≈ 0,707

 

Коэффициент гармоник

 

Коэффициент гармоник — это соотношение у_{rес и} у_{eff. Для синусоидальной кривой коэффициент гармоник равен} у_rес / у_eff  ≈ 1,111

 

Амплитудный фактор

 

Для синусоидальной кривой амплитудный фактор равен: y/y_eff = √ 2 ≈ 1,414.

 

Уравнения

 

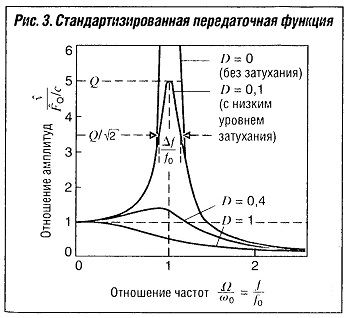
Данные уравнения применимы к следующим простым колебаниям (таблица «Простые колебательные системы» ), если общие обозначения в формулах заменить соответству­ющими обозначениями физических величин.

 

Дифференциальное уравнение

 

ay + by +су = F_Q(t) = F_Q sin Ω t

Период                  T=1/f

Угловая частота ω = 2 πf.

Синусоидальное колебание y = y sin ωt

 

Собственные колебания (F_Q = 0)

 

Логарифмический декремент (рис. «Свободные колебания и демпфирование» ):

Λ = ln(y_n/y_n+1) = πb / √ (ca — b²/4)

Коэффициент затухания δ = b/2a

Декремент D = δ / ω0 = b/2 √ca    ,

D = Λ/ √(Λ2+4π2)≈ Λ/2π (низкая степень демпфирования).

Угловая частота незатухающих колебаний (D = 0): ω₀ = √c/a .

Угловая частота затухающих колебаний (0<D<1): ω_d  =  ω₀ √ (1-D²) .

При D⩾ 1 колебания отсутствуют, только медленное перемещение.

 

Вынужденные колебания

 

Величина функции передачи:

y/f_Q = 1/√(c-aΩ²)² + (bΩ)² = 1/c√(1-(Ω/ω₀)²)² + (2DΩ/ω₀)²

Резонансная частота f_g = f₀√1-2D² <f₀,

Острота резонанса Q= 1/(2D√1-D²),

Резонансная частота f_g ≈ f₀ (при D ⩽ 0,1),

Острота резонанса Q≈ 1/2D, (при D ⩽ 0,1)

Ширина резонансного пика половинной энергии Δf =2Df₀ = f₀/Q .

 

Ослабление вибрации

 

Гашение вибраций

 

Если демпфирование вибраций может быть вы­полнено между машиной и местом, в наимень­шей степени подверженным их воздействию, то это обеспечит наибольший уровень затухания (при наибольшем декременте, см.рис. «Стандартизованная передаточная функция».

 

Виброизоляция

 

Активная виброизоляция

 

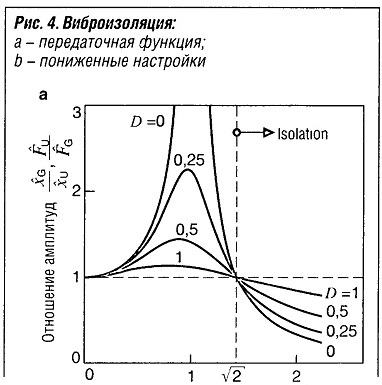
Машина должна устанавливаться на опору таким образом, чтобы силы, передающиеся на нее, были незначительными.

Необходимо выбирать опору так, чтобы кон­струкция находилась вне резонанса, и ее соб­ственная частота была бы ниже самой низкой возмущающей частоты. Затухание ухудшает виброизоляцию. Слишком низкие значения затухания могут привести к трудностям, вызванным резонансом во время разгона машины (рис. «Виброизоляция» ).

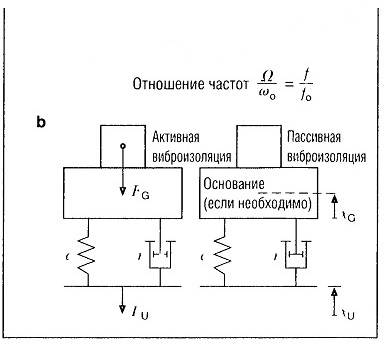Пассивная виброизоляция

 

Машина должна монтироваться таким образом, чтобы вибрация и тряска на опорах передава­лись механизмам в незначительной степени.

Принимаемые меры аналогичны случаю с ак­тивной изоляцией. Во многих случаях, гибкая подвеска или усиленное демпфирование непри­менимы. Для предотвращения возникновения резонанса, крепление машины должно быть та­ким жестким, чтобы собственная частота была намного больше самой высокой частоты воз­буждения, которая может возникнуть (рис. «Виброизоляция» ).

 

Поглощение вибраций

 

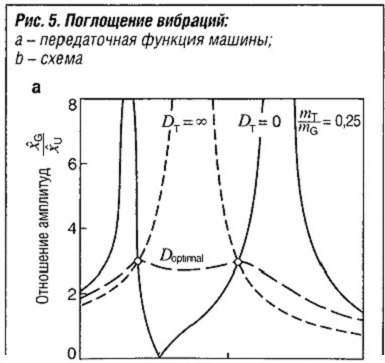
Гаситель колебаний с фиксированной собственной частотой

 

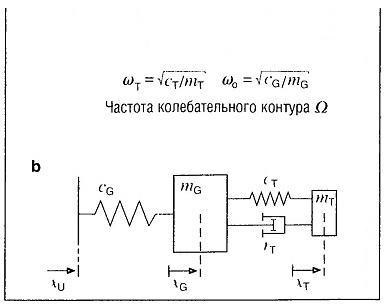
При настройке собственной частоты f_T по­глощающей массы с гибким соединением без потерь на частоту возбуждения, вибрация основной массы полностью поглощается (рис. «Поглощение вибраций» ) и продолжает вибрировать только погло­щающая масса. Эффективность поглощения снижается по мере того, как изменяется частота возбудителя. Затухание препятствует полному поглощению. Однако соответствую­щая настройка частоты гасителя колебаний и декремента оптимального затухания вызывает широкополосное ослабление вибрации, кото­рое остается эффективным при изменении частоты возбудителя.

 

Гаситель колебаний с переменной собственной частотой

 

Вращательные колебания с частотами возбуж­дения, пропорциональными частоте вращения (например, порядок уравновешивания ДВС), могут поглощаться с помощью амортизаторов с собственными частотами, пропорциональными частоте вращения (маятник в поле центробеж­ных сил). Поглощение вибраций эффективно при любых скоростях вращения. Поглощение вибраций возможно и для колебательных си­стем (осцилляторов) с несколькими степенями свободы, посредством использования несколь­ких гасителей колебаний.

 

Модальный анализ

 

Динамические характеристики (характе­ристики собственных колебаний) колеба­тельных систем определяются с помощью модального анализа. Он используется в про­ектировании, помимо прочих способов, для оптимизации конструкций с точки зрения колебательных параметров и идентификации проблемных участков, а также в акустике для анализа шумов, порождаемых конструкцией изделия).

Колебательная конструкция, которая, представляя собой сплошную среду, имеет бесконечно много степеней свободы, заменяется в явном виде конечным числом одно­массовых генераторов колебаний. Созданная таким образом модальная модель конструк­ции описывается модальными параметрами:

• Формы собственных колебаний (собствен­ный вектор или мода);
• Собственные частоты (собственные зна­чения);
• Соответствующие модальные параметры демпфирования.

 

Необходимым условием является не изме­няющаяся во времени линейно-эластичная структура. Любое колебание структуры может быть искусственно воссоздано по известным характеристическим векторам и значениям. Тем не менее, колебания наблюдаются лишь в ограниченном числе точек из возможных направлений колебаний (степеней свободы) и в определенных частотных интервалах.

Еще более детальный процесс совмещения субструктур объединяет, например, модаль­ные модели различных структур в одну об­щую модель.

 

Числовой модальный анализ

 

Для выполнения аналитического модального анализа необходимо знать геометрию модели, свойства материала и граничные условия. Осно­вой числового модального анализа является многочастичная система или конечноэлемент­ная модель конструкции. Из этого вычисляются собственные значения и собственные векторы решением задачи на собственные значения.

Числовой модальный анализ выполняется без прототипа конструкции и может использоваться уже на ранних стадиях разработки. Однако часто точных знаний о фундаментальных свойствах конструкции (демпфирование, граничные усло­вия) не хватает, и это означает, что модальная модель иногда бывает ошибочной. Кроме того, ошибка является неидентифицируемой. Одним из решений данной проблемы служит коррек­тировка модели с использованием результатов экспериментального модального анализа.

 

Экспериментальный модальный анализ

 

Для экспериментального модального ана­лиза необходим прототип конструкции. Анализ основывается на измерениях передаточных функций. С этой целью конструкция либо возбуждается в одной точке в заданном диапазоне частот, и колебательные отклики измеряются в нескольких точках, либо она возбуждается последовательно в нескольких точках, и колебательные отклики всегда из­меряются в одной точке. 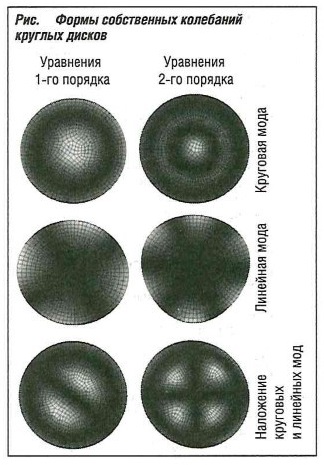Модальная модель выводится из матрицы функций передачи, которые определяют данную модель. В ка­честве средства возбуждения используется импульсный молот или электродинамический «вибратор». Отклик измеряется с по­мощью датчиков ускорения или лазерного виброметра.

Экспериментальный модальный анализ также может применяться для подтверж­дения результатов числового анализа. За­тем могут быть выполнены имитационные расчеты на достоверной числовой модели. В расчетах вычисляется ответная реакция структуры на определенное возбуждение, соответствующее, например, условиям лабо­раторного опыта.

Посредством структурных модификаций (изменения массы, затухания или жесткости) динамическое поведение может быть опти­мизировано до уровня, соответствующего действующим условиям. При сравнении мо­дальных моделей, полученных при помощи обоих способов, окажется, что аналитический модальный анализ более точен, чем экс­периментальный, за счет большего числа сте­пеней свободы. Это, в частности, позволяет проводить расчеты, основанные на модели.

Формы собственных колебаний по резуль­татам модального анализа могут быть отра­жены в графическом или анимационном виде (примеры на рис. «Формы собственных колебаний округлых дисков» ). Различные уровни се­рого показывают перемещение вертикально по плоскости проекции. Частичное искрив­ление дисков является результатом данных перемещений.  

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: