
Механика как наука описывает перемещение материальных тел и взаимодействие между ними. Эта информация требуется любому конструктору для проектирования машин и механизмов. В этой статье изложены основы двух разделов механики — кинематики (наука о движении тел) и динамики (наука о движущих силах) двигателей внутреннего сгорания (ДВС).
Двигатели с принудительным искровым зажиганием и дизельные двигатели в общем виде представляют собой как поршневые, так и роторно-поршневые машины. Оба термина подразумевают движение поршня как основу работы механизма. В поршневом двигателе (рис. «Поршневой и роторно-поршневой двигатели») поршень поступательно перемещается вперед и назад между двумя мертвыми точками — верхней и нижней. Расстояние между двумя мертвыми точками называется рабочим ходом поршня Н. На рис. «Поршневой и роторно-поршневой двигатели» схематически изображен роторно-поршневой двигатель. Здесь ротор (который выполняет роль поршня) вращается вокруг собственного центра и в то же время вращается с эксцентриситетом вокруг центра картера.
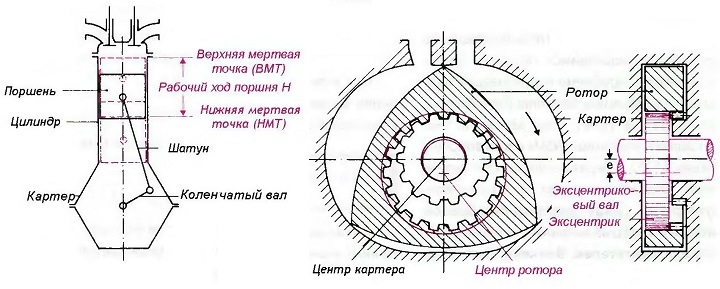
Рис. Поршневой и роторно-поршневой двигатели
Простейший поршневой двигатель состоит из поршня, шатуна и коленчатого вала. Направляющей поршня является цилиндр. Коленчатый вал размещен в картере двигателя. Преобразование кинетической энергии газов в механическую работу происходит на верхней стороне (днище) поршня. Возникающие при этом усилия передаются от поршня через шатун на коленчатый вал. В результате возвратно-поступательные движения поршня преобразуются во вращательное движение коленчатого вала, на котором возникает крутящий момент, передающийся далее на трансмиссию и ведущие колеса автомобиля.
Простейший роторно-поршневой двигатель состоит из ротора и эксцентрикового вала, размещенных в картере двигателя. На трех торцевых поверхностях ротора происходит преобразование кинетической энергии газов в механическую работу. Возникающие при этом усилия, воздействуя на торцевые поверхности ротора, приводят ротор во вращение. Крутящий момент от ротора через эксцентриковый вал передается на трансмиссию и ведущие колеса автомобиля. Поскольку направление вращения ротора не меняется, мертвые точки в механизме отсутствуют. Роторно-поршневой двигатель в сравнении с поршневым обладает следующими преимуществами:
- Не требуется преобразование возвратно-поступательного движения во вращательное;
- Не возникают свободные силы инерции.
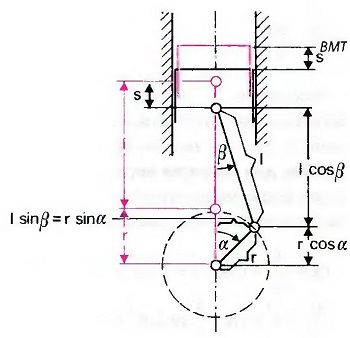
Рис. Величина перемещения поршня s
Поршень двигается между верхней и нижней мертвыми точками несогласованно, то есть с ускорением и замедлением. Коленчатый вал, напротив, вращается с постоянной угловой скоростью. Движения шатуна согласованы как с движениями поршня, так и с вращением коленчатого вала. Фактическое удаление поршня от своего положения в верхней мертвой точке (ВМТ) называется перемещением поршня s, и математически выражается как функция угла поворота коленчатого вала я (рис. «Величина перемещения поршня s»).
s = l + r — (l cos β + r cos а)
Кинематика роторно-поршневого двигателя
Ротор роторно-поршневого двигателя размещен на эксцентрике (кулачке) эксцентрикового вала (рис. «Поршневой и роторно-поршневой двигатели»). Ротор на плавающей посадке способен проворачиваться относительно эксцентрика, и в то же время вращается вместе с валом, передавая крутящий момент на вал за счет эксцентрикового механизма. Большая шестерня ротора с внутренними зубьями находится в постоянном зацеплении с небольшой неподвижной шестерней, закрепленной в картере двигателя. Эта пара шестерен не передает крутящий момент, а служит для направления движения ротора. При вращении центр ротора всегда находится на расстоянии е от центра картера. Это расстояние называется эксцентриситет. При вращении ротора его торцевые кромки описывают фигуру, которую можно назвать перециклоида или эпициклоида.
Как перециклоиду, так и эпициклоиду можно построить геометрически. В перециклоиде обкатывающая окружность обкатывает неподвижную окружность внутренней стороной, а при эпициклоиде обкатывает основную окружность своей наружной поверхностью. Условная точка, находящаяся на обкатывающей окружности, в этих случаях описывает плоскую кривую — перециклоиду или эпициклоиду (рис. «Построение профиля картера роторно-поршневого двигателя»). Оба варианта образуют одну и ту же фигуру, если соответственно выбрать радиусы окружностей и расстояния между точками.
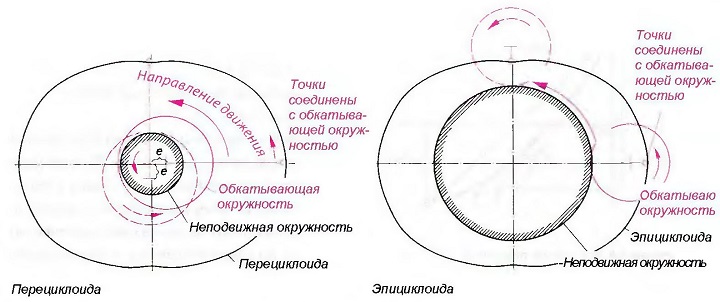
Рис. Построение профиля картера роторно-поршневого двигателя
Разумеется, строго геометрические построения требуют больших затрат времени. Определить форму картера роторно-поршневого двигателя можно быстрее, если использовать методику, представленную на рис. «Построение перециклоиды».
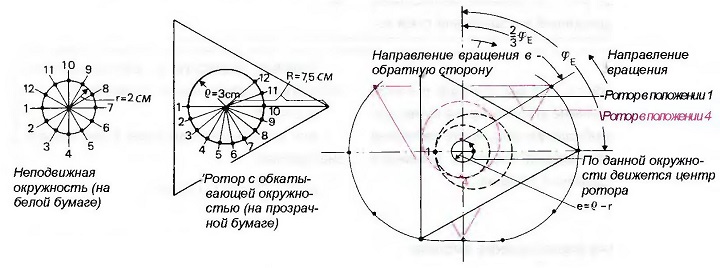
Рис. Построение перециклоиды
Для этого требуется один белый и один прозрачный лист бумаги формата А4. На белом листе бумаге необходимо нарисовать неподвижную окружность с радиусом r = 2 см, а на прозрачном листе бумаги обкатывающую окружность с радиусом r = 3 см. Для изображения обкатывания обе окружности необходимо разделить на одинаковые по размеру дуги, а точки пересечения радиусов с окружностью пронумеровать от 1 до 12. Вокруг центра обкатывающей окружности рисуется равносторонний треугольник со стороной 7,5 см, схематично представляющий собой ротор. Теперь можно начинать построение перециклоиды, то есть контура внутренней поверхности картера роторно-поршневого двигателя.
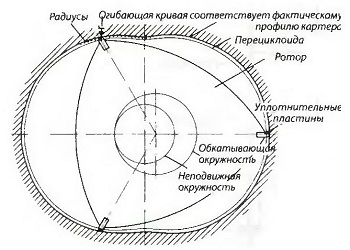
Рис. Фактический профиль картера ротоно-поршневого двигателя
При этом обкатывающая окружность должна обкатывать неподвижную окружность таким образом, чтобы совпали одинаково пронумерованные точки и радиусы окружностей. Вершины равностороннего треугольника в каждом положении прозрачного листа бумаги следует прокалывать, чтобы на белом листе бумаге оставались точки. Замкнутая кривая, проведенная через эти точки на белой бумаге, очертит требуемую перециклоиду, то есть примерный контур внутренней поверхности картера. Фактический контур картера лишь незначительно отличается от перециклоиды. Это происходит вследствие того, что ротор не имеет острых торцевых кромок по углам. На их месте размещены закругленные уплотнительные пластины, препятствующие перетеканию газов с одной стороны ротора на другую. Кривая, огибающая все отмеченные точки с учетом размера уплотнительных пластин, является фактическим профилем картера (рис. «Фактический профиль картера ротоно-поршневого двигателя»). Для дальнейшего рассмотрения мы опустим разницу между двумя типами кривых и за основу возьмем перециклоиду.
На основании графического построения, изображенного на рис. «Построение перециклоиды», можно сделать следующие выводы:
- При вращении ротора расстояние между его центром и центром картера остается всегда равным эксцентриситету е = ρ — r.
- Полному обороту ротора соответствуют три полных оборота эксцентрикового вала, так как центр ротора, совпадающий с центром эксцентрика, вращается также три раза.
- При одновременном повороте ротора с эксцентриком относительно картера двигателя на угол φЕ вал проворачивается относительно ротора на угол 2/3 φЕ. Соответственно, ротор относительно вала поворачивается на угол 1/3 φЕ .
Силы действия газов на поршень
Силы действия газов в цилиндре возникают вследствие выделения и расширения газов при сгорании рабочей смеси. Эти силы воздействует сверху на поршень, а снизу на него действует атмосферное давление (рис. «Силы действия газов на поршень»). Сила действия газов рассчитывается по формуле:
FG = A·pu
А — проекция днища поршня на поверхность, которая находится вертикально на оси поршня;
pu— избыточное давление рабочей среды.
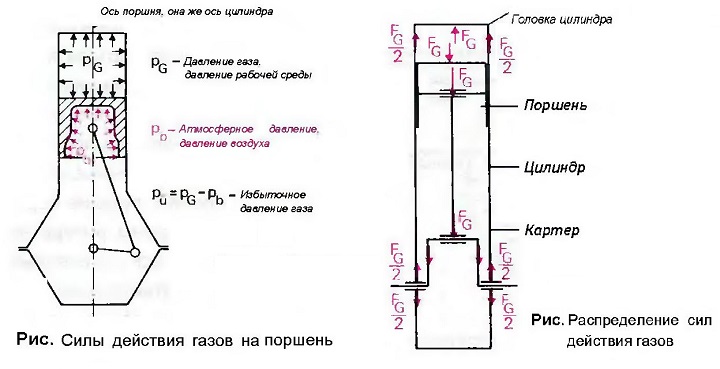
Если проследить за распределением сил, которое происходит в результате расширения газов в цилиндре, станет понятным, что не возникает никаких сил, действующих наружу, а наоборот, все силы уравновешиваются внутри мотора (рис. «Распределение сил действия газов»).
Силы инерции массы
При неодинаковом движении масс как в поршневом, так и в роторно-поршневом двигателе возникают силы инерции, которые требуется уравновесить с помощью противодействующих сил. В роторно-поршневом двигателе силы инерции уравновешиваются полностью, в поршневом же только частично. Так как силы инерции периодически изменяют величину и направление действия, при грамотном уравновешивании они не способны служить возбудителем периодических колебаний. Конструктор должен всегда стремиться к максимально возможному уравновешиванию сил инерции.
Силы инерции оказывают не только негативное воздействие. Например, противодействуя на поршне силам действия газов в цилиндре, они разгружают кривошипно-шатунный механизм.
Различают силы инерции при вращательном и возвратно-поступательном движении. Первые также называют центробежными силами. Они возникают при однообразном круговом движении масс. Для расчета центробежных сил инерции используют следующую формулу:
Fr = mr r ω2
где:
mr — вращающаяся масса;
к — расстояние от центра тяжести массы до ее центра вращения;
ω — угловая скорость.
Силы инерции при возвратно-поступательном движении вызываются, в частности, неравномерным движением поршня. Они рассчитываются по формуле:
Fos = mos · α
mos— масса, движущаяся возвратно-поступательным образом:
α — ускорение поршня.
В роторно-поршневом двигателе вследствие взаимодействия массы ротора mK, и массы эксцентрика mE, возникают только центробежные силы инерции. Обе массы вращаются с эксцентриситетом е вокруг центра картера с частотой вращения эксцентрикового вала. Формула для центробежных сил инерции роторно-поршневого двигателя является следующей:
Fr = (mK + mE) е ω2
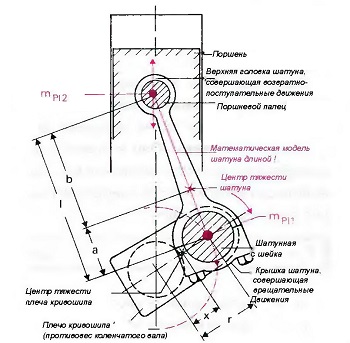
Рис. Математическая модель шатуна
В поршневом двигателе расчет центробежных сил инерции немного затруднителен. В этом случае к вращающимся массам относятся шатунная шейка, два плеча кривошипа (противовесы коленчатого вала) и вращающаяся часть (массовая доля) шатуна (рис. «Математическая модель шатуна»). Силы инерции вращающейся части шатуна определяются примерным образом с помощью математической модели шатуна длиной l, поскольку движение центра тяжести шатуна нельзя рассчитать с помощью обычных формул. Дело в том, что верхний конец шатуна, соединенный через поршневой палец с поршнем, выполняет лишь возвратно-поступательные движения, а нижний конец шатуна вращается вместе с шатунной шейкой вокруг центра коленчатого вала. Для математической модели шатуна принято считать, что ее масса mpl состоит из двух частей (массовых долей), одна из которых — mpl2 — движется возвратно-поступательным образом вместе с поршнем, а другая — трl1 — вращается вместе с шатунной шейкой.
Центры тяжести вращающихся масс кривошипно-шатунного механизма в поршневом двигателе находятся на различном расстоянии от центра вращения, поэтому для расчетов все массы снижаются на величину радиуса поршня r. При этом действительно присутствующие массы преобразовываются в условные массы, которые должны быть настолько велики, чтобы они самостоятельно вызывали возникновение центробежных сил. Формула для снижения массы следующая:
mЕ = mх х/r
mЕ —условная масса;
mх —действительная масса;
X — расстояние действительной массы от центра вращения;
r — расстояние условной массы от центра вращения.
Шатунная шейка и вращающаяся массовая доля шатуна находятся на расстоянии г от центра вращения и поэтому не должны уменьшаться. Масса плеча кривошипа, наоборот, должна уменьшаться.
Тангенциальная сила
Диаграмма тангенциальных сил для поршневого двигателя отображает тангенциальные силы через угол поворота кривошипа или через ход пальца кривошипа (в случае двигателя речь идет о шатунной шейке коленчатого вала). Величину тангенциальных сил можно определить с помощью графического метода.
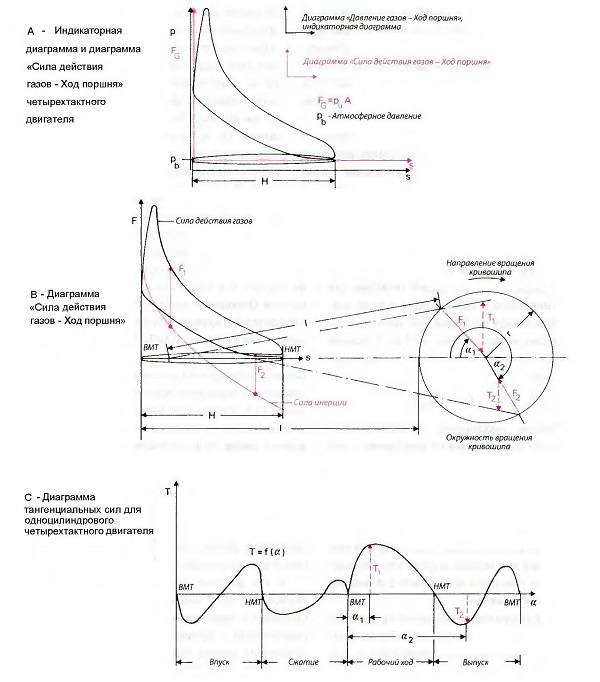
Рис. Построение диаграммы тангенциальных сил
Так как величина тангенциальных сил зависит от сил действия газов в цилиндре и от сил инерции поршня, сначала необходимо определить их величины. Силы действия газов можно определить с помощью индикаторной диаграммы. На индикаторной диаграмме давление газов в цилиндре на графике изображается над горизонтальной осью, где откладывается либо величина хода поршня, либо время (рис. «Построение диаграммы тангенциальных сил»). Индикаторную диаграмму преобразуют в диаграмму «Сила действия газов — Ход поршня» посредством изменения масштаба вертикальной оси графика (оси ординат). Именно силы действия газов являются продуктом избыточного давления газов ри в цилиндре на поверхность А поршня. В случае, когда давление на индикаторной диаграмме указывается как абсолютное, необходимо поднять горизонтальную ось (ось абсцисс) до уровня атмосферного давления (рис. «Построение диаграммы тангенциальных сил»).
Если на графике масштаб давления (масштаб черной вертикальной оси р графика «Построение диаграммы тангенциальных сил; А»), к примеру, составляет 1 см: 5 бар (в 1 см 5 бар), тогда масштаб сип действия газов (масштаб красной вертикальной оси F ) на поверхность поршня заданной площадью 50 см2 составит 1 см: 2500 Н (в 1 см 2500 Н) согласно определению 1 бар = 10 Н/см2.
На диаграмме «Сила действия газов — Ход поршня» (рис. «Построение диаграммы тангенциальных сил; В») силы инерции при возвратно-поступательном движении указываются с противоположным знаком. При этом на графике получается парабола. Здесь необходимо только умножать указанные значения ускорения на массы деталей, движущихся возвратно-поступательным образом, то есть, вместо r ω2( 1 + λ) указывается mos r ω2(1 + λ) в верхней мертвой точке (ВМТ) и т.д. При этом на диаграмме можно сразу определить равнодействующие сил действия газов и сил инерции в виде расстояния между кривыми сил действия газов и сил инерции (рис. «Построение диаграммы тангенциальных сил; В»). В основе данного определения лежит следующая формула:
F = FG+Fos=FG— (-Fos)
Дальше необходимо с соблюдением масштаба хода поршня на диаграмме «Сила действия газов — Ход поршня» (рис. «Построение диаграммы тангенциальных сил; В») изобразить окружность вращения кривошипа, то есть окружность радиусом кривошипа г, которую при вращении описывает центр шатунной шейки. Величину тангенциальных сил можно определить для каждого угла поворота кривошипа с помощью следующего метода:
- На окружности вращения кривошипа изображаются кривошипы в положениях, заданных углами поворота кривошипа α1и α2 (рис. «Построение диаграммы тангенциальных сил; В»).
- Определяется положение поршня относительно кривошипов в заданных углах поворота. Для этого из точек на окружности вращения, которые соответствуют заданным углам поворота шатуна, необходимо начертить дуги радиусом I, равным длине шатуна, до их пересечения с осью абсцисс, после чего соединить прямыми полученные точки на оси абсцисс с точками на окружности вращения. Эти прямые изображают положения шатуна, соответствующие разным углам поворота кривошипа.
- В точках пересечения определяются равнодействующие F1 и F2 (рис. «Построение диаграммы тангенциальных сил; В», слева) сил действия газов и сил инерции. Эти равнодействующие графически изображаются в виде стрелок (стрелочных указателей) между кривыми сил инерции и сил действия газов на диаграмме. Каждая стрелка лежит на вертикальной прямой, проходящей через точки на оси абсцисс, соответствующие положениям поршня при разных углах поворота кривошипа. Основание каждой стрелки всегда находится на кривой сил инерции, а вершина — на кривой сил действия газов.
- Полученные стрелки F1 и F2 в том же масштабе отображаются на кривошипах, изображенных на рисунке окружности вращения (рис. «Построение диаграммы тангенциальных сил; В», справа). Если на диаграмме «Сила действия газов — Ход поршня» стрелка указывает вверх, тогда на рисунке окружности кривошипа стрелка должна наноситься в направлении к центру вращения кривошипа. Если же стрелка на диаграмме указывает вниз, стрелка на рисунке окружности кривошипа должна наноситься в направлении от центра вращения кривошипа.
- На рисунке окружности вращения кривошипа через вершину каждой стрелки проводятся перпендикуляры T1 и T2 до пересечения с прямыми, изображающими положения шатуна при разных углах поворота кривошипа. Данные перпендикуляры также изображаются в виде стрелок и являются искомыми тангенциальными силами. Вершина стрелки всегда находится на шатуне, а основание — на кривошипе. Если стрелка направлена вверх, это означает, что тангенциальные силы положительны, то есть действуют по направлению вращения кривошипа. Если стрелка направлена вниз, то тангенциальные силы действуют против вращения кривошипа.
- Полученные величины тангенциальных сил наносятся на диаграмму тангенциальных сил (рис. «Построение диаграммы тангенциальных сил; С») в соответствии с заданными углами поворота кривошипа. Если брать размер стрелки непосредственно с рисунка окружности вращения кривошипа, то на диаграмме тангенциальных сил масштаб оси ординат, на которой откладывается величина тангенциальных сил Т, должен быть таким же, как и на диаграмме «Сила действия газов — Ход поршня». Для оси абсцисс диаграммы тангенциальных сил, разумеется, необходимо указать другой масштаб, поскольку здесь на этой оси отображается угол поворота кривошипа а. При необходимости можно принять иной масштаб и для оси ординат диаграммы тангенциальных сил. Тогда перенос данных с рисунка окружности вращения кривошипа должен производиться с соответствующим пересчетом.
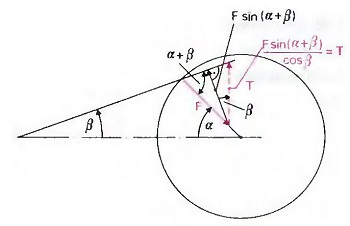
Рис. Математическое доказательство графического метода определения тангенциальных сил
Математическое доказательство того, что графический метод определения тангенциальных сил является верным, изображается на рис. «Математическое доказательство графического метода определения тангенциальных сил». Диаграмма, полученная вышеуказанным графическим методом, представляет собой изображение тангенциальных сил при работе одного цилиндра. Для двигателей с несколькими цилиндрами процедура остается неизменной. Так как диаграммы всех цилиндров одинаковы и сочетаются друг с другом сообразно разнице углов поворота кривошипа для каждого цилиндра, следует сначала начертить диаграммы для каждого цилиндра, а потом наложить их друг на друга для получения общей диаграммы тангенциальных сил многоцилиндрового двигателя.
Графический метод составления диаграммы тангенциальных сил поршневого двигателя далеко не всегда можно использовать для описания работы роторно-поршневого двигателя, поэтому для последнего необходимо сделать наброски математического способа решения.
Сначала следует начертить индикаторную диаграмму. Разумеется, давление газа должно наноситься не сообразно ходу поршня, а в соответствии с углом поворота эксцентрикового вала, что соответствует углу поворота кривошипа в обычном поршневом двигателе (рис. «Индикаторная диаграмма и диаграмма «Сила действия газа — Угол поворота эксцетрикового вала (УПЭВ) для роторно-поршневого двигателя»).
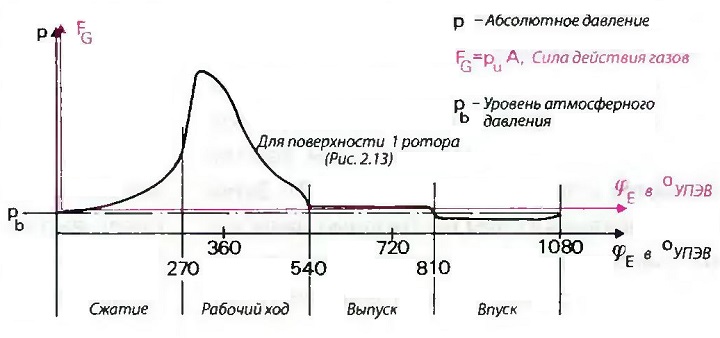
Рис. Сила действия газа — Угол поворота эксцетрикового вала (УПЭВ) для роторно-поршневого двигателя
Преобразование индикаторной диаграммы в диаграмму «Сила действия газа — Угол поворота эксцентрикового вала» выполняется так же, как и для поршневого двигателя. Так как направление действия сил инерции проходит через центр эксцентрикового вала, тангенциальные силы от них не зависят. Решающим для тангенциальных сил являются собственно силы действия газа, величина которых берется из диаграммы. Затем тангенциальные силы необходимо наносить на диаграмму сообразно углу поворота эксцентрикового вала, что даст диаграмму тангенциальных сил для одной поверхности ротора. Кривые тангенциальных сил для двух других поверхностей ротора имеют одинаковое протекание, но должны указываться со смещением на 360° или 720° от угла поворота эксцентрикового вала для первой поверхности. При наложении этих трех кривых получаем диаграмму тангенциальных сил роторно-поршневого двигателя (рис. «Диаграмма вращающих усилий роторно-поршневого двигателя»).
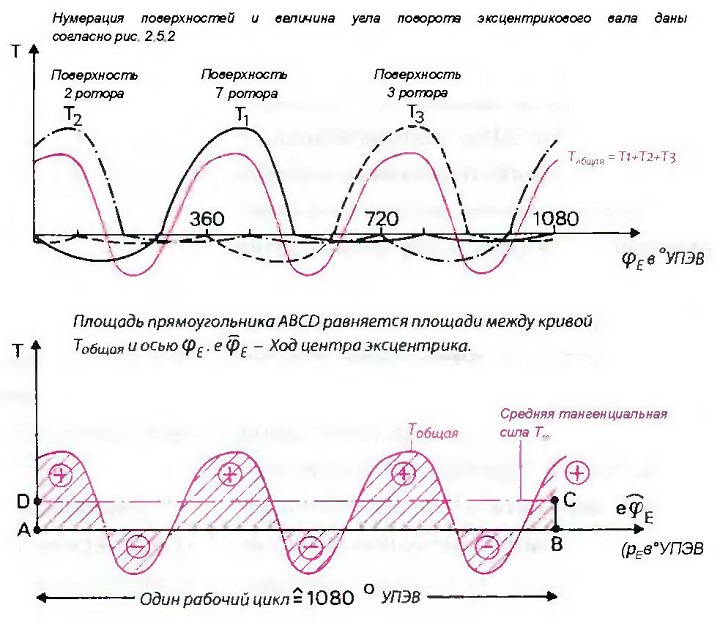
Рис. Диаграмма вращающих усилий роторно-поршневого двигателя
Если изменять масштаб оси абсцисс диаграммы тангенциальных сил в зависимости от величины угла поворота эксцентрикового вала или величины хода центра эксцентрика (либо в зависимости от величины угла поворота коленчатого вала или величины хода шейки коленчатого вала для поршневого двигателя), то можно получить диаграмму «Тангенциальная сила — Ход». На этой диаграмме ось абсцисс и кривая тангенциальных сил взаимоограничивают ряд замкнутых площадей. Если эти площади расположены над осью абсцисс, что обозначает положительную работу, то двигатель вырабатывает механическую энергию. Площади под осью абсцисс обозначают зоны, где двигатель потребляет энергию. В двигателе внутреннего сгорания, который в общем виде относится к энергетическим машинам, сумма площадей цикла работ должна быть положительной. Если преобразовать положительную сумму площадей в прямоугольник ABCD равной по размеру площади (рис. «Диаграмма вращающих усилий роторно-поршневого двигателя»), тогда его высота будет равна величине средней тангенциальной силы Тm, которая является мнимой, чисто арифметической величиной.
Коэффициент неравномерности
Величина крутящего момента поршневого двигателя постоянно меняется. Для агрегата, приводимого в движение посредством этого двигателя, наоборот, необходим постоянный крутящий момент. Например, если бы в стационарном генераторе постоянного тока крутящий момент все время изменялся, это вызвало бы колебания частоты вращения ротора генератора и, соответственно, изменения выходного напряжения. Выравнивание величины крутящего момента в подобных случаях производится путем установки маховика, который работает как энергоаккумулятор и, таким образом, удерживает частоту вращения приближенной к постоянному значению. Если крутящий момент выше, чем средний крутящий момент, частота вращения повышается лишь незначительно, и маховик поглощает энергию. Как только крутящий момент двигателя падает ниже значения среднего крутящего момента, частота вращения падает, и маховик начинает отдавать накопленную энергию. Для того, чтобы маховик действительно стал энергоаккумулятором, должны допускаться колебания частоты вращения. Величина частоты вращения является опытным значением и зависит от параметров приводимого в действие агрегата. Малые колебания частоты вращения являются более вредными при небольших частотах вращения любого вала, поэтому опытное значение принимается как отношение колебания частоты вращения к средней частоте вращения. Это соотношение именуется коэффициент неравномерности 5.
При определении коэффициента неравномерности в большинстве случаев вместо частоты вращения используют угловую скорость ω.
δ = (ωmax — ωmin)/ωm
где:
ωmax — наибольшая угловая скорость во время одного рабочего цикла;
ωmin — наименьшая угловая скорость во время одного рабочего цикла;
ωm = (ωmax + ωmin)/2 (среднеарифметическое значение).
Величина ωm рассчитывается на основании частоты вращения вала по формуле:
ωm = 2πn
Допустимый коэффициент неравномерности δ для разных агрегатов может иметь следующие опытные значения:
- Трехфазный генератор переменного тока 1/300
- Двигатель транспортного средства 1/200 Генератор постоянного тока 1/150
- Прядильная машина 1/90
- Бумагоделательная машина 1/45
- Насосы и нагнетатели 1/25
Балансировка коленчатого вала
Выше мы говорили о силах инерции. При этом указывалось, что силы инерции могут вызвать колебания, поскольку являются непостоянными. Данные колебания негативно воздействуют на подвеску и навесное оборудование двигателя, поэтому конструктор должен хорошо продумать балансировку двигателя.
В многоцилиндровых двигателях возникают не только силы инерции, но и моменты инерции. Под балансировкой понимается умелое размещение кривошипов коленчатого вала и установка на нем противовесов, что позволяет свести к минимуму силы инерции и моменты инерции.
Уравновешивание сил инерции в одноцилиндровом двигателе
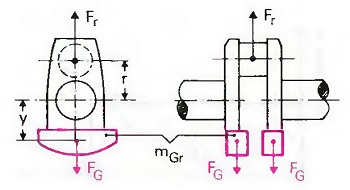
Рис. Противовесы на коленчатом валу
В одноцилиндровом двигателе моменты инерции отсутствуют, возникают только вращательные и возвратно-поступательные силы инерции.
Вращательные силы инерции уравновешиваются, как показано на рис. «Противовесы на коленчатом валу», благодаря установке на коленчатый вал двух противовесов. Размер противовеса можно рассчитать с помощью уравнения:
Fr = mr r ω2 =2 mGry ω2
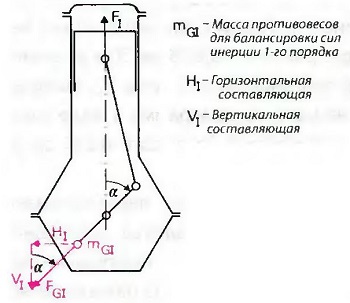
Рис. Расположение управляющей силы противовеса на вертикальную и горизонтальную составляющие
Сила инерции 1-го порядка изменяется в ритме вращения коленчатого вала, то есть в зависимости от cos а. Сила инерции 2-го порядка, наоборот, зависит от двойного угла поворота кривошипа. В результате на коленчатом валу можно уравновесить только силу инерции 1-го порядка.
Противовесы, установленные для балансировки, вращаются вместе с коленчатым валом, и для балансировки служит только вертикальная составляющая уравновешивающей силы противовеса. Горизонтальная составляющая является нежелательной мешающей дополнительной силой (рис. «Расположение управляющей силы противовеса на вертикальную и горизонтальную составляющие»). Для того, чтобы горизонтальная составляющая не была слишком большой, с помощью противовесов уравновешивается лишь 50% силы инерции 1-го порядка.
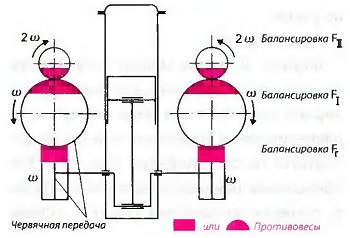
Рис. Полная балансировка в одноцилиндровом двигателе
В одноцилиндровом двигателе необходимо балансировать также силу инерции 2-го порядка. Прежде всего, необходимо понести значительные конструктивные затраты. На рис. «Полная балансировка в одноцилиндровом двигателе» представлен двигатель, в котором должны балансироваться вращательные и возвратно-поступательные силы инерции 1-го и 2-го порядков. Дополнительные валы с противовесами вращаются навстречу друг другу. Горизонтальные составляющие уравновешивающей силы противовесов обоих валов также направлены встречным образом и гасят воздействие друг друга. Валы с противовесами для балансировки сил инерции 2-го порядка вращаются с частотой, вдвое превышающей частоту вращения коленчатого вала.
Уравновешивание сил инерции и моментов инерции в однорядном двигателе
В данном разделе речь пойдет только об уравновешивании сил инерции и моментов инерции в однорядном двигателе. Данные отдельные силы объединяют только для определения равнодействующей. При хорошей балансировке сил равнодействующая будет равна нулю или же ее значение будет небольшим.
Так как отдельные силы не прикладываются к центру масс двигателя, возникают дополнительные моменты инерции, которые также должны суммироваться для равнодействующей.
Величины всех таких равнодействующих сильно зависят от формы коленчатого вала. Соответственно, вал должен быть сконфигурирован таким образом, чтобы отдельные силы сами себя уравновешивали. При решении данной задачи должны определяться равнодействующие для различных конфигураций коленчатого вала. Быстрее всего это можно выполнить, используя графический метод.
Равнодействующие вращательных сил инерции
Вначале необходимо схематически изобразить коленчатый вал в продольном и поперечном разрезе (рис. «Схема расположения кривошипов и схематический продольный разрез коленчатого вала пятицилиндрового двигателя»). Поперечное сечение, которое должно находиться слева от продольного разреза, называется из-за своего вида схемой расположения кривошипов. Нумерация кривошипов производится по продольному разрезу коленчатого вала, а затем переносится на схему расположения кривошипов.
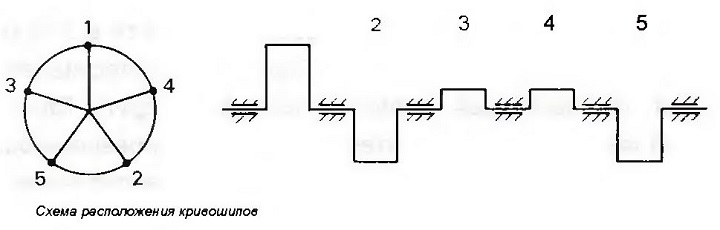
Рис. Схема расположения кривошипов и схематический продольный разрез коленчатого вала пятицилиндрового двигателя
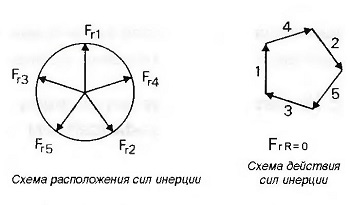
Рис. Графическое определение равнодействующей силы инерции для коленчатого вала пятицилиндрового двигателя
Затем, после выбора соответствующего масштаба, силы инерции графически изображаются на одной схеме в виде векторов. Методом векторного сложения получается схема действия сил инерции (рис. «Графическое определение равнодействующей силы инерции для коленчатого вала пятицилиндрового двигателя»), на которой отдельные силы добавляются к равнодействующей FrR и переносятся на схему расположения сил инерции (рис. «Графическое определение равнодействующей силы инерции для коленчатого вала пятицилиндрового двигателя»), которая имеет тот же вид, что и схема расположения кривошипов.
Равнодействующая FrR имеет постоянной величину. Соответственно, вектор равнодействующей на схеме будет иметь постоянную длину, и для разных положений коленчатого вала нет необходимости заново рассчитывать равнодействующую, достаточно лишь повернуть вектор на угол, соответствующий заданному углу поворота коленчатого вала.
В однорядных двигателях с равномерным порядком зажигания и более, чем двумя цилиндрами, равнодействующая равняется нулю.
Равнодействующая сил инерции 1 -го порядка
Сила инерции 1-го порядка рассчитывается по уравнению «Графическое определение значений сил инерции 1-го порядка для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания». Ее максимальное значение равно:
Flmax= mos r ω2
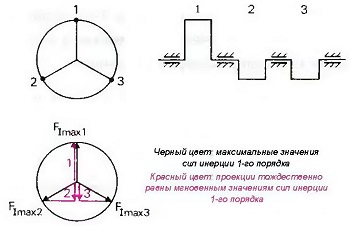
Рис. Графическое определение текущих значений сил инерции 1-го порядка
Текущее значение можно получить графически, когда максимальное значение сил инерции указывается ввиде вектора в направлении плеча кривошипа и на схеме проецируется на оси цилиндра (рис. «Графическое определение текущих значений сил инерции 1-го порядка»). При определении равнодействующей необходимо, согласно указанному способу, определить все текущие значения сил инерции 1 -го порядка, а затем векторно их суммировать. Данный способ затруднителен.
Такую равнодействующую можно получить проще, если сначала перенести все максимальные значения в виде векторов в направлении плеча кривошипа и суммировать эти силы на схеме действия сил инерции (рис. «Графическое определение значений сил инерции 1-го порядка для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания»). Полученные таким способом равнодействующие, то есть равнодействующие максимальных значений FIImaxR, проецируются на ось цилиндра. Данная проекция является искомой равнодействующей сил инерции 1 -го порядка FllR.
FIIR для трехцилиндрового коленчатого вала с неравномерным порядком зажигания.
Так как схемы действия вращательных сил инерции и сил инерции 1-го порядка похожи даже по длине векторов, очевидным является то, что при исчезновении равнодействующей вращательных сил инерции, равнодействующая сил инерции 1-го порядка будет равна нулю.
Если повернуть коленчатый вал, вместе с его поворотом изменится направление равнодействующей максимального значения. Для нового положения коленчатого вала необходимо спроецировать эту же равнодействующую максимального значения на ось цилиндра, и таким образом получить искомую равнодействующую сил инерции 1 -го порядка.
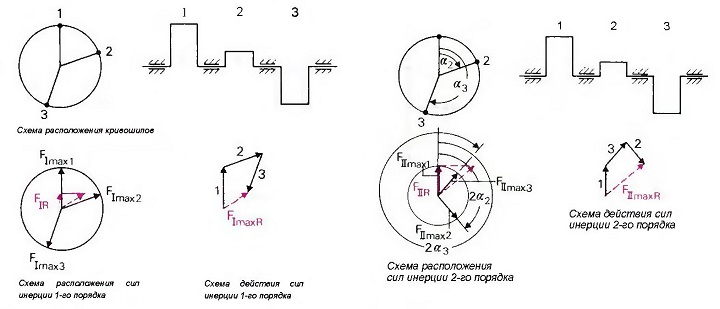
| Рис. Графическое определение значений сил инерции 1-го порядка для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания | Рис. Графическое определение значений сил инерции 2-го порядка для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания |
Равнодействующая сил инерции 2-го порядка
Сила инерции 2-го порядка рассчитывается по уравнению «Графическое определение значений сил инерции 2-го порядка для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания». Возникновение сил инерции 2-го порядка происходит в соответствии с удвоенной частотой вращения коленчатого вала. При этом на оси цилиндра эта сила действует как сила инерции 1-го порядка.
Для определения равнодействующей так же, как и в случае определения сил инерции 1-го порядка, максимальные значения каждой отдельной силы переносятся на схему расположения сил инерции (рис. «Графическое определение значений сил инерции 2-го порядка для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания»). Данные силы не совпадают из-за «cos 2α» с плечом кривошипа на схеме расположения кривошипов. На схеме расположения сил инерции 2-го порядка все силы должны наноситься сообразно удвоенной величине угла α. На схеме действия сил инерции они складываются, образовывая равнодействующую максимального значения FIImaxR все вместе переносятся на схему расположения сил. Проекция равнодействующей максимального значения FIImaxR на вертикальную ось цилиндра является искомой равнодействующей сил инерции 2-го порядка FIIR.
Если повернуть коленчатый вал на угол α равнодействующая максимального значения повернется на схеме расположения сил на угол 2α. Новая искомая равнодействующая является ее проекцией на ось цилиндра.
Результирующий момент инерции
Так как силы инерции имеют плечо относительно центра тяжести двигателя, возникают моменты инерции, которые рассчитываются путем умножения силы на расстояние (величину плеча) от центра тяжести. Для их точного определения сначала надо определить положение центра тяжести двигателя. Чаще пренебрегают данной трудоемкой работой и принимают в качестве центра тяжести двигателя точку в центре коленчатого вала. Исходной, или базовой, точкой для расчета моментов инерции считается центр коленчатого вала, определенный на продольном разрезе вала. Точно также, как и силу, момент инерции можно представить в виде вектора.
Величина момента инерции в графическом изображении выражается вектором рассчитанной длины. Вектор располагается перпендикулярно плоскости действия момента и своей вершиной указывает направление, в котором перемещался бы болт с правой резьбой, если бы его вращали по направлению действия момента.
Крутильные колебания
Коленчатый вал является подвижной деталью, в которой возникают периодические колебания. Существуют как монолитные конструкции, так и составные коленчатые валы. Периодическая изменчивая внешняя сила, влияющая на такую механическую систему, способна возбуждать вынужденные колебания. Если частота возбуждения вынужденных колебаний достигает собственной частоты вращения коленчатого вала, возникает явление резонанса, то есть эффекта наложения вынужденных и собственных колебаний системы, амплитуда колебаний при котором становится очень большой. Нагрузка, увеличивающаяся вследствие возбуждения колебаний, не должна превышать усталостную прочность коленчатого вала, в противном случае неизбежна поломка.
На коленчатом валу могут возбуждаться три вида колебаний:
- Продольные колебания — вал периодически перемещается вдоль продольной оси;
- Колебания при изгибе — вал периодически изгибается относительно своей продольной оси;
- Крутильные колебания — вал периодически подвергается ускорению и замедлению собственного вращения относительно продольной оси.
Крутильные колебания являются самыми опасными, так как они чаще всего приводят к излому коленчатого вала. В данном разделе речь пойдет именно о крутильных колебаниях и о предотвращении последствий их возбуждения. Во избежание резонанса следует проводить соответствующие расчеты, которые зачастую выполняет специалист по колебаниям. Резонанс опасен тем, что, даже не приводя к поломке коленчатого вала, вызывает опасные рабочие состояния — нарушенную балансировку, повышенный износ шестерен приводов и гул при работе. При расчетах необходимо учитывать следующие проблемы:
- Формы собственных колебаний и собственные частоты вращения коленчатого вала;
- Места возникновения резонанса и критическую частоту вращения коленчатого вала;
- Амплитуды колебаний и внутренние напряжения, возникающие при колебаниях в материале коленчатого вала;
- Меры для предотвращения недопустимо высокой частоты крутильных колебаний. Для разъяснения некоторых важных терминов вначале рассмотрим простой торсион, который состоит из вала, прочно зафиксированного с одной стороны (с жесткой заделкой), и некой массы (маховика) на свободном конце (рис. «Простой торсион»). Примем условием, что вал имеет собственную исчезающе малую массу в сравнении с маховиком, поэтому общая масса и общий момент инерции J сосредоточены в маховике. Эластичность при вращении конструкции обеспечивается валом, который имеет соответствующую жесткость на кручение, характеризуемую коэффициентом жесткости с:
c=IpG/l
Ip — полярный момент инерции площадей вала;
G — модуль упругости при сдвиге;
l — длина вала.
Коэффициент жесткости равен значению крутящего момента, при котором вал поворачивается на угол ω, величина которого характеризуется соотношением arc ω = 1. Если маховик повернуть, отклонив от положения покоя, вся система колеблется вокруг своей продольной оси. Конец вала вместе с маховиком при этом периодически поворачивается под углом ω в обе стороны. Максимальный размах колебаний называется амплитудой колебаний А. Для случая колебаний при вращении амплитуда выражается через угол ω как окружное перемещение (рис. «Простой торсион»):
А = ωr
Самые большие амплитуды колебаний приходятся на конец вала с маховиком. К месту жесткой заделки амплитуды снижаются до нуля. Здесь находятся узлы колебаний. Если изобразить амплитуду колебаний как некий график вдоль оси вала, можно получить изображение формы колебаний (рис. 2.34).
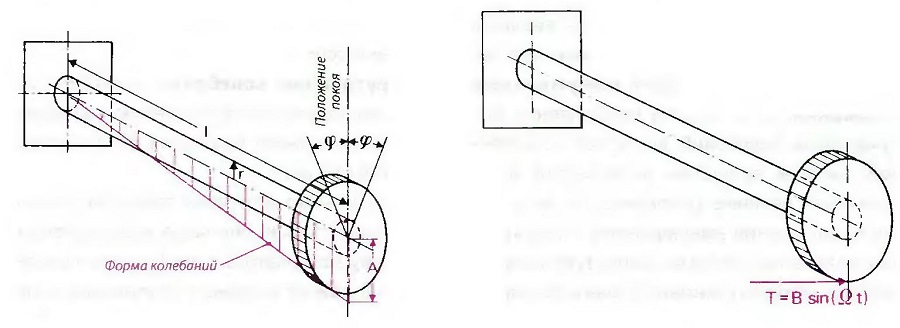
| Рис. Простой торсион | Рис. Внешнее возбуждение посредством периодической изменчивой тангенциальной силы Т |
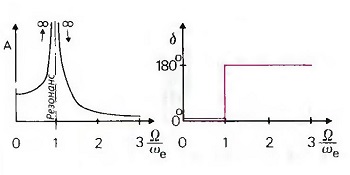
Рис. Амплитуда А колебаний, возбуждаемых внешней силой, и фазовый угол δ между силой возбуждения и колебаниями
Кроме собственных колебаний, существуют колебания, вызванные или возбуждаемые внешними силами. При этом периодическая изменчивая тангенциальная сила Т постоянно воздействует на колеблющуюся систему (рис. «Внешнее возбуждение посредством периодической изменчивой тангенциальной силы Т»). Количество колебаний в секунду больше не будет равно собственной частоте, а система, наоборот, будет колебаться с частотой возбуждения Регг тангенциальной силы. Амплитуда колебаний, которая зависит при свободном колебании от начального отклонения маховика, определяется при колебании, вызванном внешней силой, на основании амплитуды тангенциальной силы В и соотношения угловой частоты Ω/ωe (Ω= 2 π veer). При соотношении Ω=ωe возникает резонанс, а амплитуда колебаний А станет теоретически бесконечно большой (рис. «Амплитуда А колебаний, возбуждаемых внешней силой, и фазовый угол δ между силой возбуждения и колебаниями»).
В действительности амплитуда остается конечной, так как в любой колеблющейся системе возникает амортизация от трения либо от сопротивления материала колеблющейся детали. При этом энергия колебаний при трении преобразуется в тепло и, таким образом, уменьшает амплитуду колебаний.
При затухающих колебаниях, вызванных внешним воздействием, амплитуда колебаний зависит не только от соотношения угловой частоты, но и от величины амортизации. На рис. «Амплитуда А затухающих колебаний, вызванных внешним воздействием» представлены амплитуды колебаний для сильной и слабой амортизации. Амплитуда колебаний растет до того момента, пока энергия силы возбуждения не будет равна энергии, отводящейся из системы с помощью амортизации.
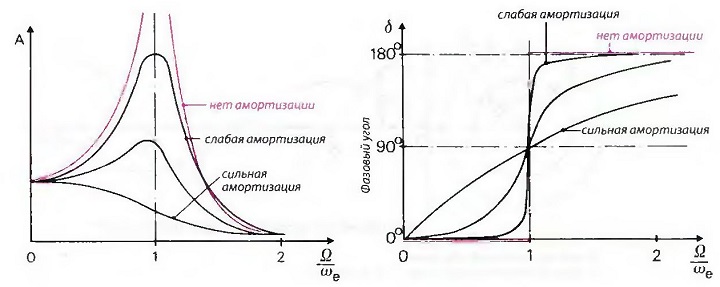
Рис. Амплитуда А затухающих колебаний, вызванных внешним воздействием
При незатухающих колебаниях, вызванных внешним воздействием, сила и амплитуда колебаний совпадают по фазе, до тех пор, пока соотношение угловой частоты Ω/ωe < 1. Для Ω/ωe > 1 несовпадение силы и амплитуды происходит со сдвигом фазы на 180°. При этом при растущем Ω/ωe амплитуда колебаний становится все меньше.
Сдвиг фазы можно объяснить лучше всего с помощью векторной диаграммы (рис. «Векторная диаграмма»). С помощью одного вращающегося вектора, который вращается с заданной частотой, можно легко определить параметры колебания. Угловая частота колебания равна угловой скорости вектора. Угол между вектором В тангенциальной силы и вектором А амплитуды колебаний равен углу сдвига фазы или фазовому углу δ.
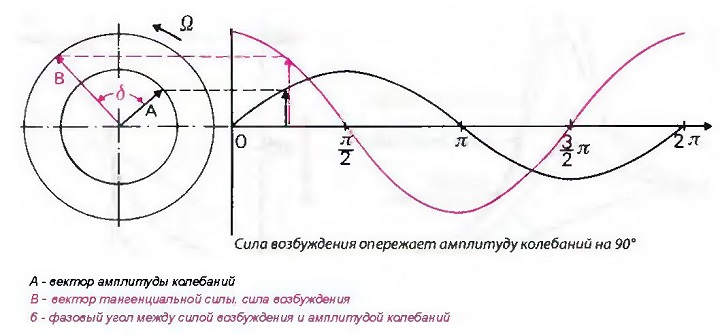
Рис. Векторная диаграмма
При затухающих колебаниях, вызванных внешним воздействием, сдвиг фазы между тангенциальной силой и амплитудой колебаний зависит от соотношения угловой частоты и величины амортизации (рис. «Амплитуда А затухающих колебаний, вызванных внешним воздействием»). Если амортизация незначительная, возникает максимальная амплитуда колебаний как при незатухающих колебаниях при резонансе, то есть Ω/ωe = 1. Сила возбуждения при этом опережает амплитуду колебаний на 90°, то есть совпадает по фазе со скоростью колебаний. В данном состоянии колеблющаяся система получает максимум энергии через силу возбуждения.
Теперь рассмотрим возможные колебания коленчатого вала. Необходимо определять форму собственных колебаний и собственную частоту колебаний. Так как коленчатый вал из-за своей сложной формы не позволяет выполнить непосредственные расчеты колебаний, необходимо создать равноценную математическую модель для расчета колебаний. Главная задача специалиста по колебаниям состоит в том, чтобы разработать математическую модель на основании размеров коленчатого вала и соединенных с ним деталей.