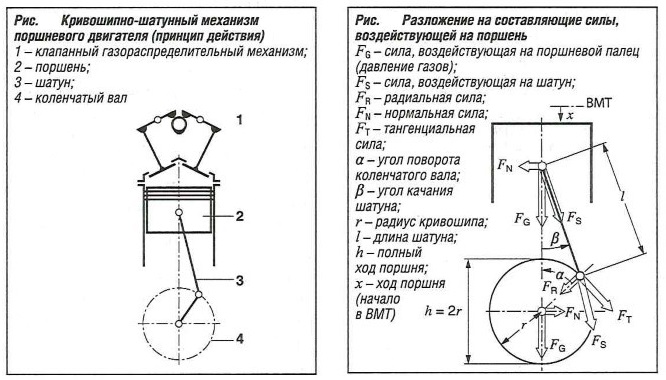
Коленчатый вал является одной из важных деталей двигателя. Он преобразует поступательное движение поршня во вращательное движение, которое в дальнейшем, через трансмиссию, передается к колесам.

 

 

Кинематика привода коленчатого вала

 

Кинематика привода коленчатого вала (для одного цилиндра) может быть определена из геометрического расположения осей поршня и поршневого пальца, шатуна и коленчатого вала (радиус коленчатого вала равен половине рабочего хода поршня) (см. рис. «Кривошипно-шатунный механизм поршневого двигателя» ).

 

 

Если ход поршня х в верхней мертвой точке принять равным нулю, при радиусе кривошипа r и длине шатуна l получаем (см. рис. «Разложение на составляющие силы воздействующей на поршень» ):

х = r ( 1 — cosa) + l (1 — cosβ),

где:

r·sina = l·sinβ и λ = r/l.

Получаем следующее:

x = r (1 — cosa + 1/λ (1- √‾1-λ²·sin²a))

Некоторые производители применяют компо­новку со смещенным поршневым пальцем. За счет изменения положения поршня и в зави­симости от положения шатуна можно ожидать снижения трения и уровня шума. Смещение может осуществляться путем сдвига поршне­вого пальца относительно центрального поло­жения или смещения коленчатого вала.

Если принять смещение для положительных углов поворота коленчатого вала положи­тельным и ввести величину

δ = смещение / длина шатуна

это дает следующее соотношение для хода поршня:

x=r (1 — cosa + 1/λ (1- √‾1-(λ·sina-δ)²).

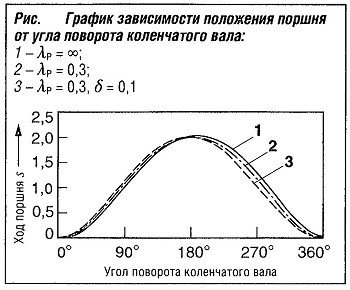
На рис. «График зависимости положения поршня от угла поворота коленчатого вала» показано влияние отношения хода поршня к длине шатуна и смещения. Однако различия по сравнению с нормальными зна­чениями смещения в миллиметровом диапа­зоне (δ< 0,04), заметно меньше.

Преобразуя корневую функцию в ряд Тэйлора (при значениях хода около х = 0: в ряд Маклорена) и заменяя степени тригоно­метрических функций полигармоническими функциями, можно получить следующее вы­ражение:

х = r(1+1/4·λ+3/64·λ³+…- cosa-(1/4λ+3/64·λ³+…)cos2a+(3/64·λ³+…)cos4a+…)

Это выражение демонстрирует присутствие высших гармоник, обусловленных кинематикой привода коленчатого вала, которые также назы­ваются колебаниями двигателя высшего порядка (кратные частоты вращения коленчатого вала).

Поскольку нормальные значения λ состав­ляют около 0,3, членами λ высшего порядка можно пренебречь и в дальнейших расчетах ис­пользовать следующее упрощенное выражение:

х = r( 1 +  1/4λ — cosа —   1/4λ · cos2а) .

Однако это упрощение не может быть ис­пользовано, если необходимо выполнить детальный анализ вибрации и резонанса.

Из упрощенного уравнения получаются следующие соотношения для скорости поршня v и ускорения поршня а, где была введена угловая скорость da/dt=ω= 2πn (п частота вращения):

v = rω (sin а + λ/2 · sin2а)

а = rω² (cosa + λ·cos2а).

Здесь также имеют место высшие гармоники, которые не следует игнорировать при иссле­довании явлений резонанса.

 

Динамика коленчатого вала

 

Силы, воздействующие на узел коленчатого вала, и результирующие моменты первона­чально можно определить следующим обра­зом без учета сил инерции (рис.»Разложение на составляющие силы воздействующей на поршень» ).

Сила на поршневом пальце возникает под действием давления газов в камере сгорания, передающегося на поршень. Имеет место следующее:

F_G = (P -P_KGH) A_piston 

Сила на шатуне определяется посредством векторного анализа силы на поршневом пальце в направлении шатуна. Имеет место следующее:

F_S = F_G /cosβ=F_G /√¯1-λ²·sin²a

Нормальная сила поршня F_N — это векторная составляющая силы на поршневом пальце, перпендикулярная к стенке цилиндра и урав­новешивающая силу на шатуне:

F_N=F_G·tanβ=F_G·λ sina/√¯1-λ²·sin²a

Эта сила вносит значительный вклад в соз­дание трения между поршнем и стенкой цилиндра. Сторона, с которой соприкаса­ется поршень после верхней мертвой точки под действием давления газов, называется большой упорной поверхностью, а противо­положная сторона — малой упорной поверх­ностью. Следовательно, наибольшее трение имеет место вскоре после прохождения ВМТ на большой упорной поверхности.

Тангенциальная сила на шатунной шейке коленчатого вала вызывает ускорение ко­ленчатого вала и, следовательно, увеличение крутящего момента коленчатого вала. Она определяется путем векторного анализа силы на шатуне:

F_T=F_Gsin(a+β) / cosβ= F_G (sin a + λ/2·sin2а/√‾1 -λ²sin²a).

Подкоренное выражение может быть упро­щено следующим образом:

F_T≈ F_G (sinа + λ/2· sin2а) .

Радиальная сила F_R на шатунной шейке ко­ленчатого вала:

F_R =F_G·cos(a+β)/cosβ

или приблизительно

F_R≈ F_G (cosa — λ/2+λ/2·cos2a) .

Силы инерции можно разделить на коле­бательные и вращательные составляющие. Массы поршня, поршневых колец и поршне­вого пальца m_к относятся к колебательной составляющей и могут быть виртуально со­средоточены в поршневом пальце.

Щека коленчатого вала с шатунной шейкой относятся к вращательной составляющей. Здесь масса обычно сосредотачивается на радиусе кривошипа, на центральной оси ша­тунной шейки. Применимо следующее:

m_w=Σ m_lr_sl/r

где m_l — масса соответствующего компонента (щека, палец и т.д.), а r_sl — соответствующий радиус центра массы.

В связи с колебательным движением ша­туна целесообразно разделить массу шатуна на колебательную и вращательную составляю­щие. Это может быть сделано, если известно точное положение центра тяжести и момента инерции шатуна, предполагая наличие двух динамически идентичных отдельных масс ма­лой и большой головок шатуна, и определяя Условие равновесия сил, моментов и инерци­онных масс. Обычно предполагается, что одна треть массы шатуна т_pl является колебатель­ной, а две трети — вращательной. Затем при т₀ = m_K + 1/3 т_Рl, как колебательной массы и со­ответствующем ускорении поршня (см. ниже) колебательная сила инерции выражается как:

F₀≈m₀·r·ω² (cosa + λ·cos2a),

Таким образом, колебательная сила инерции возрастает пропорционально квадрату ча­стоты вращения двигателя (ω = 2π·п) и имеет составляющую первого порядка и меньшую составляющую второго порядка.

Вращательная сила инерции выводится, как центробежная сила из уменьшенной массы m_r = m_w + 2/3 т_Рl и скорости враще­ния как:

F_r = m_r·r·ω²

Точно так же вращательная сила инерции воз­растает пропорционально квадрату частоты вращения двигателя, но не имеет составляю­щих высших порядков. Вращательная сила инерции, следовательно, может быть легко уравновешена противовесами, вращающимися со скоростью, равной частоте вращения двига­теля. Неравномерности вращения коленчатого вала столь малы по сравнению с этими силами, что в балансе масс ими можно пренебречь.

Как было показано выше в кинематике узла коленчатого вала, высшие гармоники (колебания высшего порядка) возникают за счет геометрии кривошипно-шатунного ме­ханизма. Амплитуда колебаний 4-го и выше порядков быстро снижается, и в балансе масс этими колебаниями, как правило, пре­небрегают.

 

Уравновешивание масс в одноцилиндровом двигателе

 

Компонент вращающейся массы в одноци­линдровом двигателе может быть полностью уравновешен при помощи соответствующего противовеса. Противовесы обычно преду­сматриваются на обеих сторонах, и массы должны быть сбалансированы относительно радиуса вращения центра масс. Колебания сил можно представить в виде векторов силы (рис. «Полностью уравновешенные массы 1-го и 2-го порядков» ), когда они моделируются как вращающиеся в противоположных направле­ниях, и имеющие в каждом случае половин­ную величину.

 

 

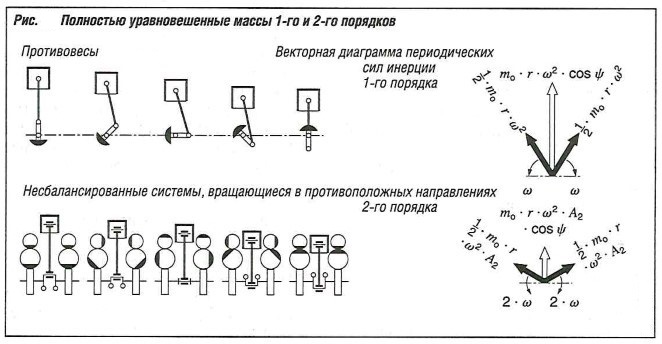
Следовательно, для уравновешивания коле­бательных сил инерции могут быть использо­ваны два вращающихся в противоположном направлении вала. Горизонтальная составля­ющая исчезает и, как минимум составляющая колебательной силы инерции первого порядка может быть скомпенсирована.

Для практически полного уравновешивания масс требуются дополнительные уравновешивающие валы, которые должны вращаться со скоростью в два раза выше частоты вращения двигателя, чтобы полностью уравновесить со­ставляющую колебаний второго порядка.

Часто конструкторам приходится идти на ком­промисс вследствие того, что системы с противо­положно вращающимися валами являются до­рогостоящими, и уже для уравновешивания сил инерции первого порядка требуются значитель­ные массы. Например, масса противовеса может быть равна половине колеблющейся массы. При этом неуравновешенные силы инерции, дей­ствующие наружу в направлении продольной оси цилиндра, уменьшаются наполовину, однако за счет больших масс, вращающихся компонен­тов возникают поперечные силы (см. табл. «Уравновешивание масс в одноцилиндровом двигателе, в зависимости от степени уравновешивания» ). Такая частичная компенсация называется 50% — ной балансировкой. Обычными цифрами явля­ются 100% уравновешивание вращающихся масс и 50% уравновешивание колеблющихся масс.

 

 

Уравновешивание масс в многоцилиндро­вых двигателях

 

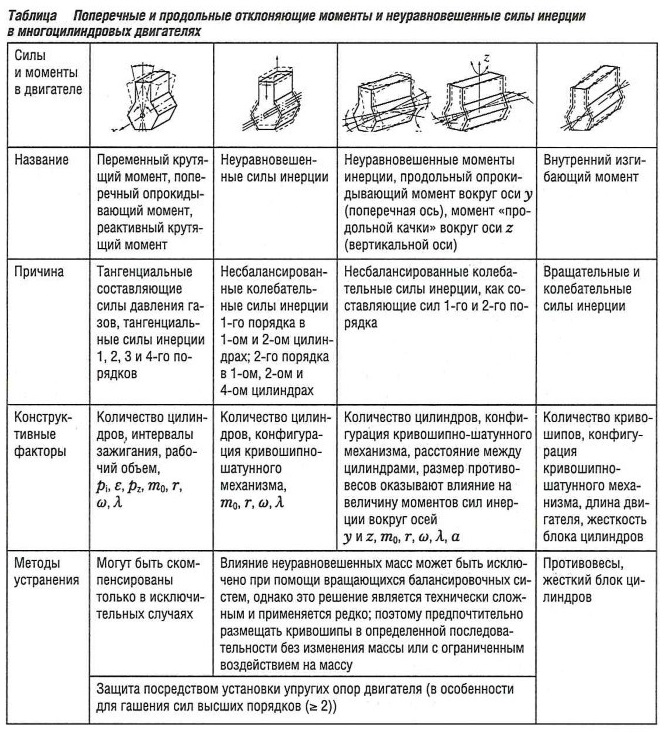
В многоцилиндровом двигателе силы инер­ции состоят из сил инерции каждого отдель­ного цилиндра, которые накладываются друг на друга. Кроме того, за счет промежутков между цилиндрами создаются неуравнове­шенные моменты инерции. Все возможные поперечные и продольные отклоняющие моменты, и неуравновешенные силы инерции показаны в табл. «Поперечные и продольные отклоняющие моменты и неуравновешенные силы инерции в многоцилиндровых двигателях» .

 

 

Взаимное уравновешивание сил инерции яв­ляется одним из главных факторов, определя­ющих выбор конфигурации коленчатого вала, а, следовательно, и конструкции самого дви­гателя. В многоцилиндровых двигателях силы инерции могут быть уравновешены, если об­щий центр тяжести всех деталей кривошипно-шатунного механизма располагается в средней точке коленчатого вала, т.е., если коленчатый

вал является симметричным (глядя спереди). Это представлено полярными диаграммами сил 1-го и 2-го порядка (см. табл. «Полярная диаграмма сил для рядных двигателей» ).

 

 

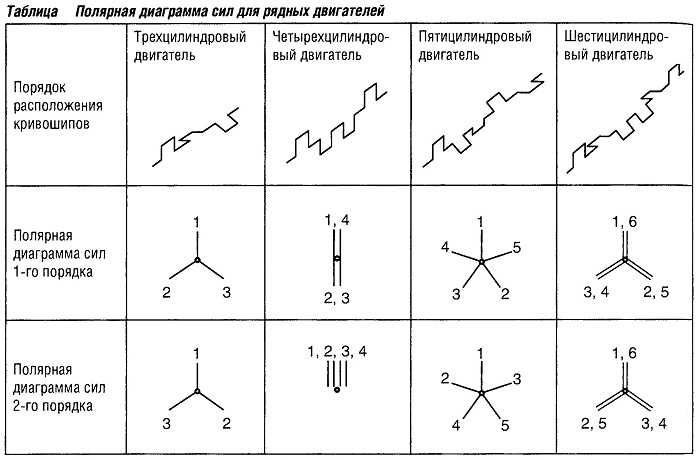
Диаграмма 2-го порядка для четырех­цилиндрового рядного двигателя является асимметричной, указывая на то, что этот порядок характеризуется наличием больших неуравновешенных сил инерции. Эти силы могут быть уравновешены двумя балансир­ными валами, вращающимися в противопо­ложных направлениях, но с удвоенной часто­той (система Ланчестера).

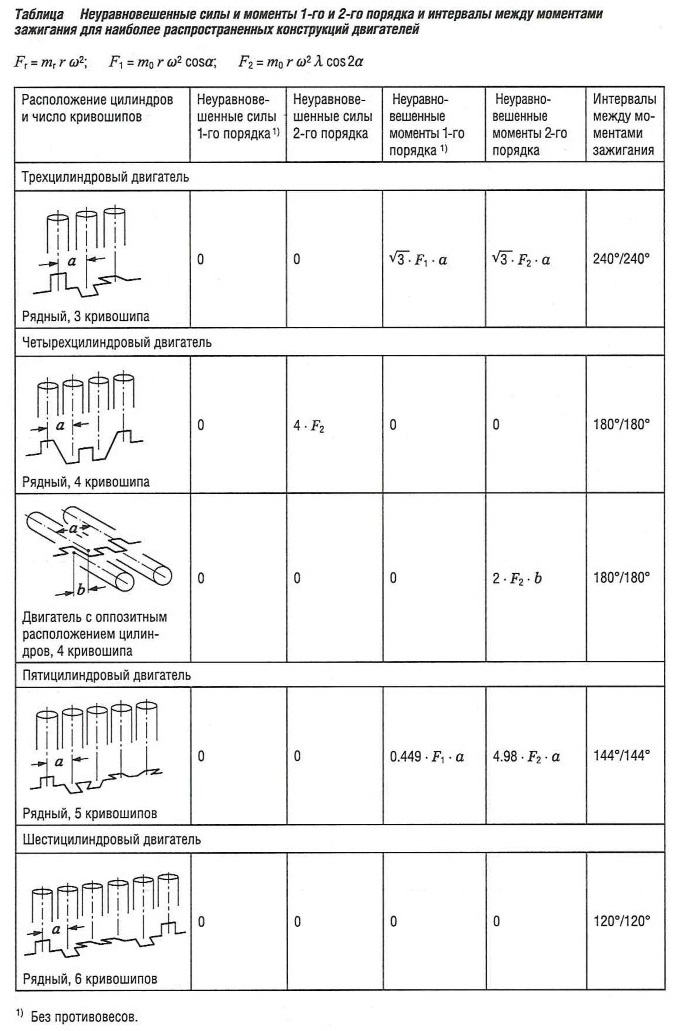
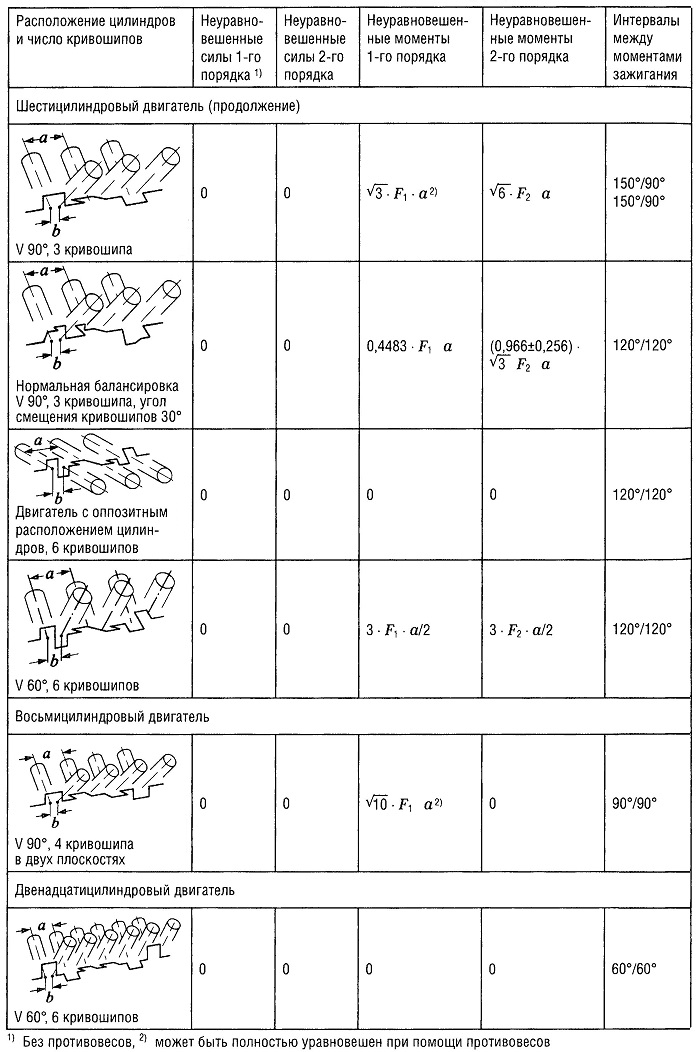
В табл. «Неуравновешенные силы и моменты 1-го и 2-го порядка и интервалы между моментами зажигания для наиболее распространенных моделей двигателей» приведена сводка неуравнове­шенных сил и моментов для различного числа цилиндров и конфигураций кривошипно-шатунных механизмов.

 

 

Крутящая сила

 

Массы в двигателе движутся с постоянно из­меняющимся ускорением, что приводит к возникновению сил инерции. Циклически из­меняющиеся давления в цилиндрах называ­ются силами газообразных продуктов сгора­ния смеси. Те и другие силы по отношению к двигателю имеют как внутренние, так и внеш­ние составляющие. Внутренние силы и мо­менты должны поглощаться компонентами двигателя, в особенности коленчатым валом и картером двигателя, в то время как внешние силы через опоры двигателя передаются на шасси автомобиля.

На поршень действуют циклические уси­лия, создаваемые при сгорании топливовоздушной смеси, а циклические инерционные усилия действуют на поршень, шатун и ко­ленчатый вал. Все эти силы в сумме создают тангенциальную составляющую силы, дей­ствующую на шейку коленчатого вала. Эта сила, умноженная на радиус кривошипа, дает крутящий момент, также изменяющийся по периодическому закону.

 

В многоцилиндровых двигателях кривые тангенциального давления для отдельных ци­линдров суммируют в соответствии с числом цилиндров двигателя, их расположением, кон­струкцией коленчатого вала и порядком ра­боты цилиндров. Полученная результирующая кривая является характеристикой двигателя (с точки зрения его конструкции) и включает весь рабочий цикл (т.е., для четырехтактных двига­телей два оборота коленчатого вала) (см. рис. «Полностью уравновешенные массы 1-го и 2-го порядков» ). Этот процесс можно проиллюстрировать диаграммой крутящих сил. Эта переменная крутящая сила и результирующий крутящий момент, в зависимости от момента инерции J, создают переменную скорость вращения ω:

dω/dt = M(t)/J

с учетом всех наложенных и вновь создан­ных порядков колебаний (в том числе по­ловинных порядков). Это отклонение от постоянной скорости вращения называется коэффициентом циклического изменения скорости вращения и определяется следую­щим образом:

δ_s = (ω_max — ω_min) / ω_min

Этот коэффициент циклического измене­ния может быть уменьшен до приемлемого уровня при помощи механизмов, запасаю­щих энергию, таких как, например, маховики. Крутильные колебания, которые можно от­следить назад к описанным выше крутящим силам, также называются крутильными колебаниями 1-го порядка. Эти колебания нельзя смешивать с высокочастотными ко­лебаниями, возникающими вследствие упру­гих деформаций и собственного резонанса коленчатого вала, называемыми колебаниями 2-го порядка.

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: