Магнитное поле образуется движущимися элек­трическими зарядами, токонесущими проводни­ками, намагниченными телами или переменным электрическим полем. Магнитное поле проявля­ется в его действии на движущийся электрический заряд (сила Лоренца) или в образовании магнит­ных диполей (одноименные полюса отталкива­ются, разноименные полюса притягиваются). Вот о том, как работает магнитное поле в автомобиле, мы и поговорим в этой статье.

 

 

Магнитное поле

 

Магнитное поле характеризуется вектором магнитной индукции В. Проводник, находя­щийся под силой тока I₁ создает на расстоя­нии а магнитную индукцию, величина которой определяется по формуле:

B = B₁ = μ₀·I₁ / 2π·a

Эта магнитная индукция притягивает второй параллельно расположенный проводник дли­ной l, по которому проходит электрический ток I₂, с силой

F=B₁I₂l

Магнитная индукция может быть определена путем измерения напряжения, возникающего при изменении магнитного поля в петлевом проводнике:

U = dФ/dt

где:

dФ — изменение магнитной индукции в пет­левом проводнике;

dt  -изменение времени.

Магнитная индукция В находится в следующей зависимости с магнитным потоком Ф (q — площадь поперечного сечения):

Ф = Вq

Зависимость магнитной индукции в вакууме от напряженности магнитного потока Н опреде­ляется уравнением:

H = B/μ₀

 

Магнитное поле и вещество

 

В материальной среде магнитная индукция B тео­ретически состоит из двух компонентов. Один воз­никает от приложенного поля (μ₀·H), другой — от материальной среды (J) (см. также взаимосвязь между плотностью электрического смещения и напряженностью электрического поля).

B=μ₀H+J

где J — магнитная поляризованность, харак­теризующая вклад материальной среды в магнитную индукцию. Физически J обозна­чает магнитный дипольный момент каждой единицы объема и в целом является функцией напряженности магнитного поля Н. Для мно­гих материалов J>>μ₀Н и пропорциональна Н. Тогда:

В=μ_rμ_оН

где  μ_r — относительная магнитная проницае­мость; в вакууме  μ_r=1

Величина

w_m = 1/2 BH

называется плотностью энергии магнитного поля. При ее умножении на объем получается энергия магнитного поля W_m.

В соответствии со значением относительной магнитной проницаемости материалы делятся натри группы:

• Диамагнитные материалы. μ_r не зависит от напряженности магнитного поля и составляет менее 1; значения находятся в диапазоне (1-10^-5)<μ_r<(1-10^-11). Например, Ag, Au, Cd, Си, Нд, Pb, Zn, вода, органические материалы, газ.
• Парамагнитные материалы. μ_r не зависит от напряженности магнитного поля и составляет более 1; значения находятся в диапазоне (1 +10^-8)< μ_r<(1 +10^-4). Например, О2, Al, Pt, Ti.
• Ферромагнитные материалы. У ферромагнитных материалов магнитная поляризация до­стигает очень высоких значений и меняется в зависимости от напряженности магнитного поля Н нелинейно. Также эти материалы характеризуются гистерезисом намагничи­вания. Тем не менее, если выбирается, как это принято в электротехнике, соотношение В=μ_rμ_оН, то μ_r является функцией H и имею­щегося гистерезиса, значения для μ_r находятся в диапазоне 10² <μ_r< 5·10⁵. Например, Fe, Со, Ni, феррит.

 

Петля гистерезиса

 

Петля гистерезиса (рис. «Петля гистерезиса для твердого феррита» ), показывающая зависимость между В и H, также как и между J и H, объясняется следующим образом: если материал находится в немагнитном состоянии (В = J = 0, H = 0), под действием магнитного поля H он намагничивается в соответствии с кривой (1). 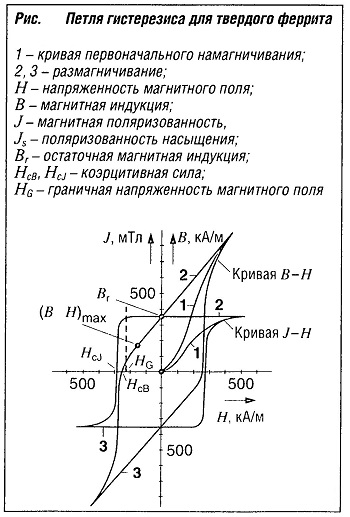Когда при некоторой напряжен­ности магнитного поля все магнитные диполи переориентируются, J достигает состояния по­ляризованности насыщения J_s (в зависимости от материала), которая не может больше повы­шаться. Если H уменьшается, J уменьшается в соответствии с кривой (2), которая уже не проходит через нулевую точку при Н = 0, а пересекает ось В или J в точке остаточного магнетизма В_r или J_r (в этом случае B_r = J_r). Индукция и поляризованность падают до нуля при обратном направлении поля только при достижении напряженности магнитного поля значения H_сВ или H_cj. Эта напряженность поля называется коэрцитивной силой. При дальнейшем повышении напряженно­сти поля достигается насыщение поляризации в противоположном направлении. Если напря­женность поля снова снижается и поле меняет направление, то симметрично отрезку кривой (2) проходит отрезок кривой (3).

Важнейшими параметрами петли гистере­зиса являются:

• Поляризованность насыщения J_s;
• Остаточная магнитная индукция В_r (остаточ­ная индукция для H = 0);
• Коэрцитивная сила H_сВ (размагничивающая напряженность поля при В = 0);
• Коэрцитивная сила H_cj (размагничиваю­щая напряженность поля при J = 0, имеет значение только для магнитотвердых ма­териалов);
• Граничная напряженность поля H_G (до этой напряженности магнитотвердые материалы остаются стабильными);
• Максимальная магнитная проницаемость ртах (максимальный подъем кривой перво­начального намагничивания, имеет значе­ние только для магнитомягких материалов);
• Потери гистерезиса (потери энергии в ма­териале в течение одного цикла перемагничивания, соответствуют площади петли гистерезиса В-Н, имеет значение только для магнитомягких материалов).

 

Ферромагнитные материалы

 

Ферромагнитные материалы подразделяются на магнитомягкие и магнитотвердые. Необхо­димо подчеркнуть, что воздействию коэрци­тивной силы подвергаются каждые восемь из десяти таких материалов.

 

Магнитотвердые материалы

 

Магнитотвердые материалы имеют высокую коэрцитивную силу. Ее значения находятся в области:

H_cj > 1 кA/м

Вместе с этим может возникнуть большое раз­магничивающее поле H, из-за которого мате­риал теряет свою магнитную поляризацию. Маг­нитное состояние и рабочая область постоянного магнита лежат во втором квадранте петли гисте­резиса на кривой размагничивания. На практике рабочая точка постоянного магнита никогда не лежит в точке остаточного магнетизма, так как из-за саморазмагничивания магнит всегда ис­пользуется в размагничивающем поле, которое сдвигает рабочую точку во второй квадрант.

 

 

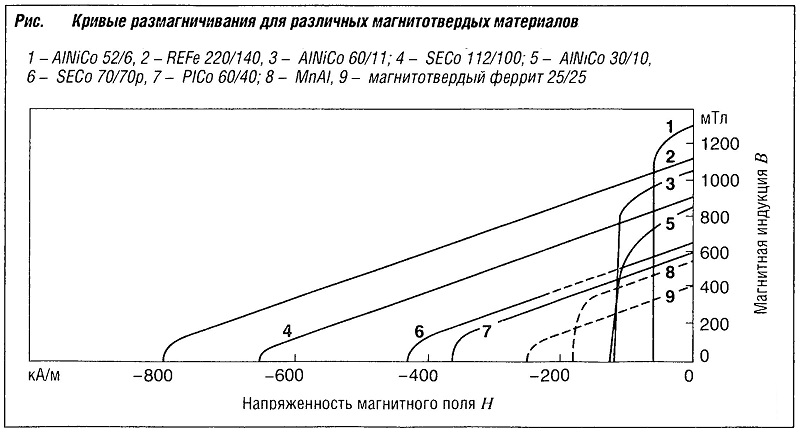
Точка на кривой размагничивания, в которой произведение В·Н достигает максимального значения (В·Н)_maх, характеризует максимально достижимую энергию в воздушном зазоре. Эта величина, в дополнение к остаточной магнитной индукции и коэрцитивной силе, имеет важное зна­чение для характеристики постоянных магнитов. Важнейшими магнитотвердыми материалами для промышленного применения являются магниты, состоящие из AINiCo, феррита, FeNdB (REFe) и SeCo; их кривые размагничивания (рис. «Кривые размагничивания для различных магнитотвердых материалов» ) демонстрируют типичные характери­стики для отдельных типов магнитов.

 

Магнитомягкие материалы

 

Магнитомягкие материалы имеют низкую ко­эрцитивную силу:

H_cj < 1 кА/м

и узкую петлю гистерезиса. Магнитная индук­ция принимает высокие значения (большие значения μ_r) уже при небольших величинах напряженности поля, так что обычно J >>μ_r·Н, то есть практически нет необходимости делать различие между кривыми В(Н) и J(H).

Магнитомягкие материалы, из-за высокой индукции при низкой напряженности магнит­ного поля, применяются в качестве магнито- проводов. Так как эти материалы показывают низкие потери при перемагничивании (потери на гистерезис), они, имея низкую коэрцитив­ную силу, отлично подходят для применения в переменных магнитных полях.

 

 

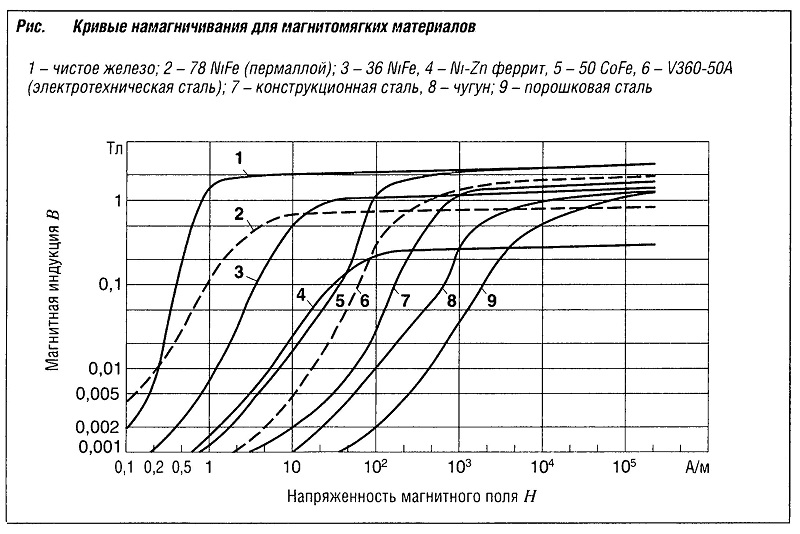
Характеристики мягкомагнитных материа­лов существенно зависят от их предваритель­ной обработки. Механическая обработка повы­шает коэрцитивную силу, а петля гистерезиса становится шире. Во избежание этого при­меняется специальный отжиг материала при высоких температурах (магнитный финальный отжиг). На рис. «Кривые намагничивания для магнитомягких материалов»  представлены кривые на­магничивания, выражающие зависимость В-Н, для нескольких важных магнитомягких материалов.

 

Потери на перемагничивание

 

В таблице «Потери на перемагничивание» даны потери на перемагничива­ние Р1 и Р1,5 для индукции в 1 и 1,5 Тл при частоте 50 Гц и температуре 20 °С.

 

 

Эти потери состоят из потерь на гистерезис и потерь от вихревых токов. Потери от вихревых токов вы­зываются напряжением, которое индуцируется в сердечнике при изменении магнитного по­тока. Уменьшение потерь от вихревых токов и снижение электрической проводимости могут быть выполнены за счет применения:

• Сердечника из листа;
• Легированных материалов (например, фер­росилиция);
• Разделения на гранулированные частицы (порошок) в области высоких частот;
• Керамических материалов (феррита).

 

Магнитное поле и электрический ток

 

Магнитное поле создается движущимся элек­трическим зарядом, то есть оно образуется вокруг проводника с электрическим током. Направление электрического тока (⊗ — ток течет в страницу, О — ток течет от страницы) и направление магнитной силовой линии под­чиняются правилу буравчика правого винта. В таблице «Напряженность магнитного поля для различного расположения проводников» приведены данные напряженности магнитного поля при различном расположении проводников.

 

 

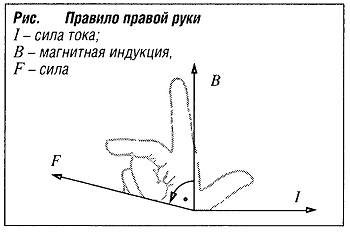В магнитном поле с индукцией В на провод длиной l с проходящим по нему электрическим током I действует сила F. Если провод и поле находятся под углом а друг к другу, сила равна:

F = B·I·l·sina

Направление этой силы можно определить с помощью правила правой руки (рис. «Правило правой руки» ): если большой палец расположить по направлению силы тока, указательный палец — по направ­лению магнитного поля, то средний палец по­кажет направление силы.

 

Закон электромагнитной индукции

 

Любое изменение магнитного потока Ф, пере­секающего петлевой проводник, например, при движении петли или при изменении силы поля, индуцирует в петлевом проводнике на­пряжение U_I. 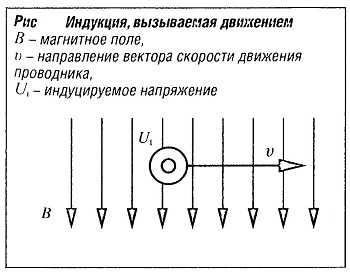Также напряжение U_I, индуцируется в проводнике, движущемся в магнитном поле в направлении v (рис. «Индукция, вызываемая движением» ):

U_I = Bvl,

где:

В — магнитная индукция;

l — длина проводника;

v — скорость.

 

Для двигателя постоянного тока:

U_I = 2(fzF/a)

 

где:

U_I — индуцируемое напряжение, В;

Ф — магнитный поток, создаваемый обмоткой возбуждения, Вб;

z — число проводников на поверхности якоря;

а — половинное число параллельных ветвей обмотки;

f — частота;  f=pn/ 60;

р- число полюсов;

п — частота вращения, мин^-1.

 

Для двигателя переменного тока:

U_I = πfzФ/√2)

где:

UI — эффективное значение индуцируемого напряжения, В;

Ф — магнитный поток, создаваемый обмоткой возбуждения, Вб;

f — частота;  f=pn/60;

р — число полюсов;

п — частота вращения, мин^-1;

z — число проводников на поверхности якоря.

 

Для трансформатора:

U₁ = 2πfw₁Ф, U₂ = 2πfw₂Ф

где:

U₁, U₂ — эффективные значения индуци­руемых напряжений, В;

Ф — эффективное значение магнитного по­тока Ф(t), Вб;

f- частота, Гц;

w₁, w₂ — число витков соответственных об­моток, пересекаемых магнитным потоком Ф.

В зависимости от времени поток Ф(t) пред­ставляет собой результат наложения значений силы тока i₁(t) и i₂(t):

Ф(t) = A_L(w₁i₁(t) + w₂i₂(t))

A_L называют AL-параметром — он зависит от конструкции трансформатора.

Выходное напряжение U на зажимах меньше (для генератора) и больше (для двигателя), чем U_I, — за счет омических потерь напряжения в обмотках (примерно 5 %).

 

Самоиндукция

 

Магнитное поле проводника или обмотки ме­няется при изменении протекающего по ним электрического тока. За счет этого в прово­днике индуцируется напряжение, пропорцио­нальное изменению электрического тока:

U = d(L_I)/dt

Индуктивность L зависит от магнитной про­ницаемости μ_r, которая для большинства ма­териалов практически равна 1 и постоянна. Исключение составляют ферромагнетики. Поэтому для обмоток с ферромагнитным сер­дечником L в значительной степени зависит от условий работы. В таблице «Индуктивность для различного расположения проводников» приведены значения индуктивности L для проводников различного расположения.

 

 

При низких частотах индуктивность прово­дников увеличивается за счет внутренней ин­дуктивности L_I проводов. Для круглых кабелей:

L_I = μ₀l/8π

Двухжильные кабели, состоящие из двух кру­глых проводов, имеют двойное значение вну­тренней индуктивности (2 L_I) на единицу длины l.

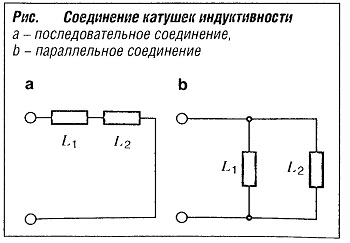
Индуктивность катушек, соединенных после­довательно и параллельно, равна:

L_total = L₁ + L₂(последовательное соединение, рис. а, «Соединение катушек индуктивности» );

1/L_total = 1/L₁ + 1/L₂  (параллельное соединение, рис. Ь, «Соединение катушек индуктивности» ).

Энергия магнитного поля для катушки с ин­дуктивностью L, по которой проходит элек­трический ток I, равна:

W = 1/2L·I²

Примеры:

(L постоянна во времени):

• постоянный электрический ток I: —> напряжение U= 0;

• начальный электрический ток I₀, напряже­ние постоянного тока U: —> сила тока I =I₀ + U t,
• синусоидальный электрический ток I = î·sin (ωt): —> косинусоидальное напряжение U=ω L î cos(ωt), U=ω L î sin(ωt + π/2),

где:

ω=2πf- угловая частота;

î — амплитуда силы тока;

û =ωL î — амплитуда напряжения.

Часто также используются эффективные зна­чения u_eff = û/√2 и i_eff = î/√2.

 

При протекании через катушку индуктивности переменного (гармонического) электрического тока векторы напряжения и электрического тока сдвинуты на угол ω = +π/2. Это свойство иллюстрирует векторная диаграмма (рис. «Векторная диаграмма катушки индуктивности» ).

Особый случай возникает, когда катушка ин­дуктивности подключается к сопротивлению, установленному со стороны источника напря­жения постоянного тока U₀, или отключается от сопротивления. Решающим фактором на­растания или падения электрического тока в цепи является постоянная времени τ = L/R.

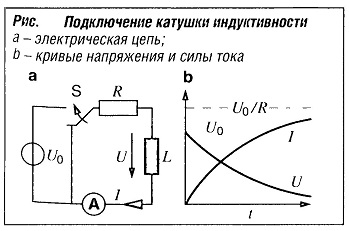При подключении катушки (рис. «Подключение катушки индуктивности» ):

U= U₀e^-е/τ

I=U₀ /R(1-e^-е/τ )

При отключении катушки:

I = I₀e^-е/τ

U = I₀R·e^-е/τ

где:

U₀— напряжение возбуждения;

I- сила тока, протекающего по катушке;

_I0 — сила тока, протекающего по катушке, при отключении;

R — сопротивление резистора, последова­тельно соединенного с катушкой;

U— напряжение на катушке.

Электрический ток при подключении и отклю­чении катушки протекает по ней в противопо­ложных направлениях.

 

Магнитная цепь

 

В дополнение к уравнениям существуют за­коны расчета магнитных цепей:

• Закон Ампера (закон полного электрического тока)

для магнитной цепи действует следующее равенство:

∑H_I·L_I = ∑V_I = Iw

где:

Iw = Θ — магнитодвижущая сила (алгебраическая сумма ампер-витков);

H_I·L_I = V_I — разность магнитных потенциалов (H_I·L_I служит для расчета компонентов цепи, при котором H_I, является постоянной).

• Закон непрерывности (принцип непрерыв­ности магнитного потока)

Магнитный поток Ф = В·А состоит из потоков на отдельных участках магнитной цепи.

Ф = const, для всех участков цепи, А — пло­щадь поперечного сечения соответствующего участка.

Магнитный поток, проходящий через участок цепи, можно разбить на частные потоки Ф₁,Ф₂…, сумма которых в любом случае будет равна постоянному значению общего потока Ф.

Качество магнитных цепей определяется замыканием магнитного потока при его про­хождении через рабочий воздушный зазор, имеющийся в цепи. Этот поток называется рабочим. Поток рассеяния, замыкаемый вне того места, где используется рабочий поток, представляет собой разность между общим и рабочим потоками. Отношение потока рас­сеяния к суммарному потоку (для постоянного магнита или электромагнита) называется ко­эффициентом рассеяния σ (практическая ве­личина σ находится в диапазоне от 0,2 до 0,9).

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: