Гидромеханика изучает равновесие и движение жидкости. Кроме того, к ней относится взаимодействие между жидкостью и телами, погруженными в жидкость полностью либо частично, а также движущимися в жидкости. Вот о том, что такое гидродинамика в автомобилестроении, мы и поговорим в этой статье.

 

 

Гидромеханика — Основные принципы 

 

 

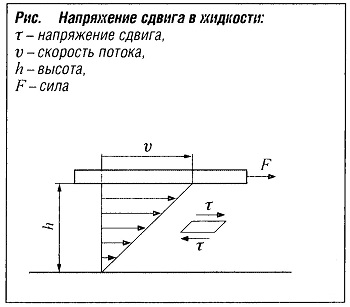Идеальная жидкость — несжимаемая и невязкая. Это означает, что в ней отсутствуют напряжения сдвига, а давление на элемент жидкости действует одинаково по всем на­правлениям. Однако фактически, если происходит деформация, вызванная смещением элементов жидкости, в ней должно преодо­леваться сопротивление (рис. «Напряжение сдвига в жидкости» ). Результи­рующее напряжение сдвига определяется по формуле Ньютона:

τ = F/A = η (ʋ/h)

Коэффициент пропорциональности η , называемый динамической вязкостью, в большой степени зависит от температуры. На практике часто используется кинематическая вязкость

ν = η/ρ

так как ее можно очень легко определять с помощью капиллярного вискозиметра.

Поток без турбулентности, в котором смежные слои жидкости движутся раздельно и парал­лельно друг другу, и который в основном определяется вязкостью, называется лами­нарным. Если скорость потока превышает не­кое предельное значение, в смежных слоях начинают образовываться водовороты, и по­ток становится турбулентным. Кроме скорости потока, переход ламинарного потока в турбу­лентный также зависит от числа Рейнольдса:

R_e = ρLʋ/η = Lʋ/ν

При движении потока по трубе величина L в данной формуле принимается за диаметр трубы. Поток в трубе становится нестабиль­ным или турбулентным при R_e> 2300.

Поскольку при движении газового потока с низкой скоростью (меньше скорости звука в 0,5 раза и ниже), сжатие незначительно, такой поток принимается за течение несжимаемой жидкости.

 

Гидромеханика — основные уравнения

 

Наиболее важными в гидромеханике являются уравнения неразрывности и Бернулли. Этими основными уравнениями описываются законы сохранения массы и энергии в потоке жидкости.

 

Уравнение неразрывности

 

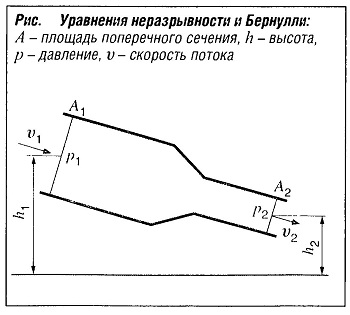При установившемся состоянии удельный массовый расход, в соответствии с законом сохранения массы, должен быть одинаковым при любом поперечном сечении потока (рис. «Уравнение неразрывности и Бернули» ):

m=ρA₁v₁ = ρA₂v₂ = const.

Для несжимаемых жидкостей (р = const.), объемный расход должен быть также постоянным:

Q = A₁v₁ =A₂v₂ = const.

 

 

Уравнение Бернулли

 

Из уравнения неразрывности следует, что между А₁ и А₂ имеет место ускорение. В результате возрастает кинетическая энергия, что сопровождается падением давления р₁ > р₂ (рис. «Уравнение неразрывности и Бернули» ). В соответствии с законом сохранения энергии сумма статического давления р, кинетического давления и геодезического давления в потоке текущей жидкости является постоянной. Если не учитывать потери на трение, поток жидкости в наклонной трубе описывается выражением:

p₁+1/2 (ρv₁²)+pgh₁ = p₂+1/2 (ρv₂²)+pgh₂ 

 

Вытекание жидкости из резервуара под давлением

 

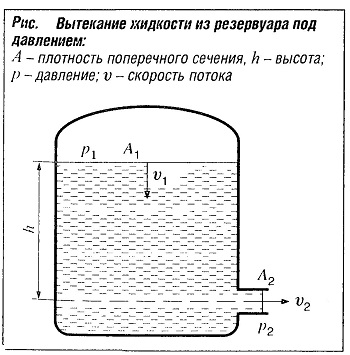Если соблюдается предварительное условие о том, что поперечное сечение выпускного отверстия намного меньше размеров резервуара (рис.«Вытекание жидкости из резервуара под давлением» ), то в соответствии с уравнением не­разрывности скорость v₁ пренебрежимо мала. Согласно уравнению Бернулли, скорость вытекания равна:

v₂ = φ√(2/ρ(p₁-p₂) + 2gh).

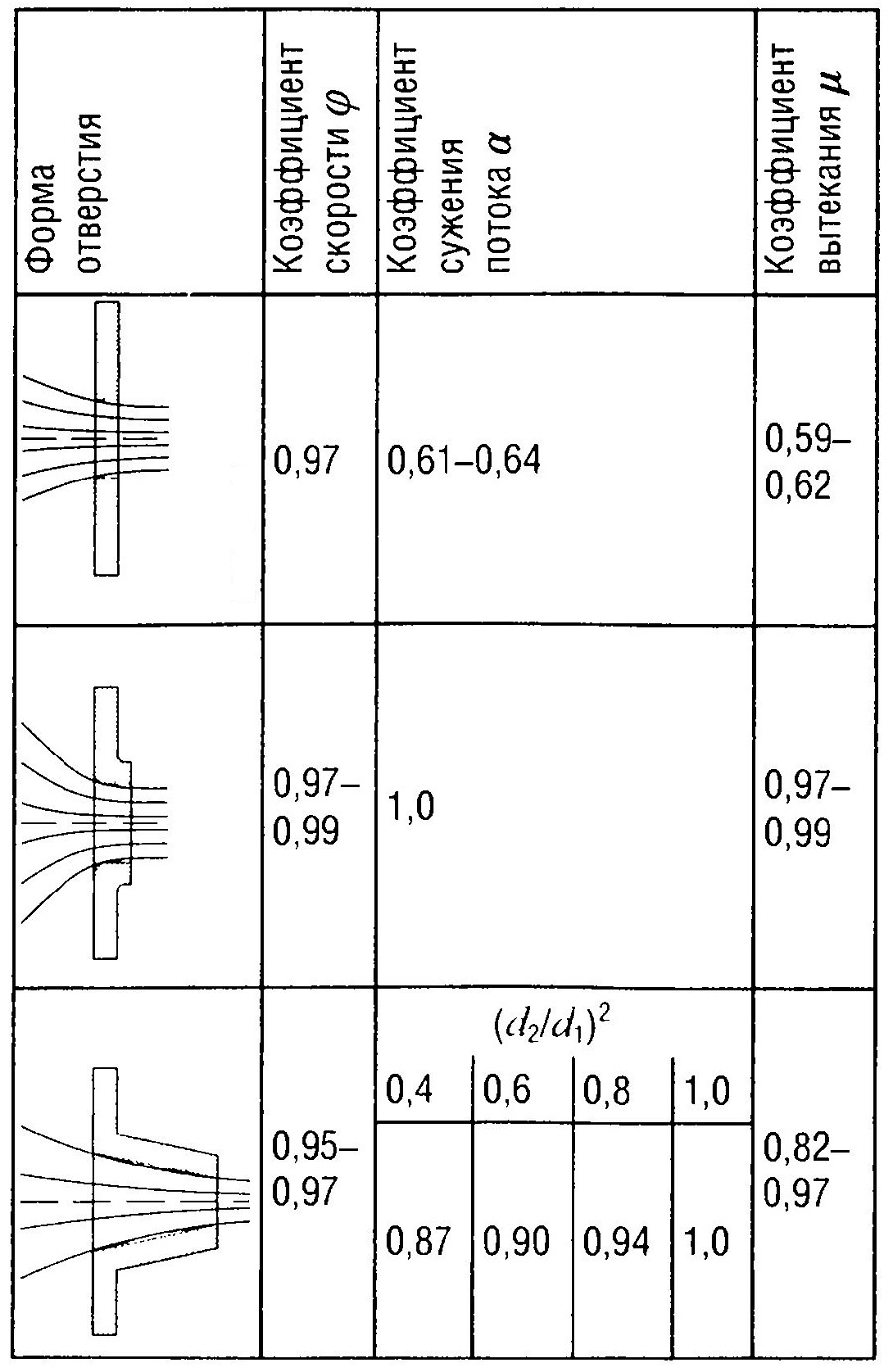
Коэффициент скорости φ учитывает потери. Также при определении объемного расхода или объема истечения должно учитываться сужение струи; это сужение определяется коэффи­циентом сужения потока а. Объемный расход с учетом коэффициента сужения потока равен:

Q = a·φ·A₂√(2/ρ·(p1-p2) + 2g·h)

Коэффициент скорости и коэффициент сужения потока часто выражаются через коэффициент вытекания μ = аφ (табл. «Выпускные отверстия» ).

 

 

Сопротивление тел, находящихся в потоке жидкости

 

Сила сопротивления тела (например, кузова), погруженного в поток жидкости, равна:

F_w = 1/2(c_wAρv²),

где:

А — площадь поперечного сечения тела, на которое воздействует поток жидкости;

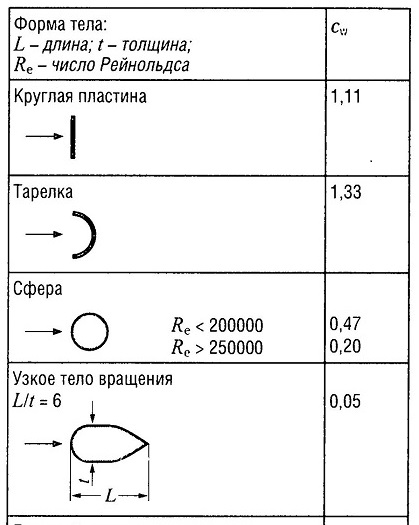
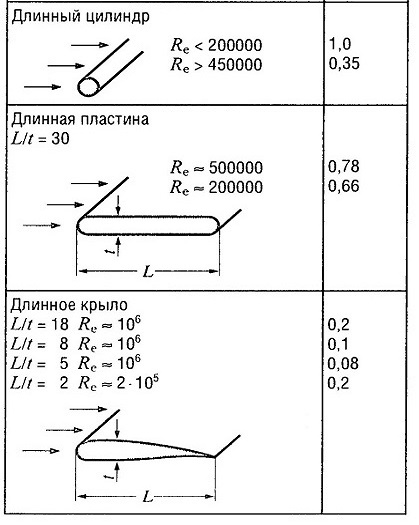
c_w — коэффициент гидродинамического со­противления, зависящий от формы тела, на­ходящегося в потоке жидкости.

Поскольку точно рассчитать сопротивление потоку даже простых тел очень сложно, со­противление потоку обычно определяется экспериментальным путем. Если размеры тел большие, то измерения проводятся на масштабных моделях. Из-за геометрического подобия величины энергии (кинетическая энергия, работа трения) в исходном и смоде­лированном потоках должны быть пропор­циональны. Эта пропорциональность обозна­чается числом Рейнольдса.

В основном, два потока в гидродинамиче­ских выражениях одинаковы, если их числа Рейнольдса равны. Поскольку что даже сложные геометрические тела состоят из простых базовых фигур, обтекаемые поверхности могут быть смоделированы с использо­ванием таких фигур, показанных в табл. «Коэффициент гидравлического сопротивления c_w«.

 

 

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: