В электротехнике рассматриваются электромагнитные поля и их действие. Эти поля вы­зываются электрическими зарядами (в каждом случае состоящими из множества элементар­ных электрических зарядов). В физике, при рассмотрении совокупности электрического и магнитного полей, не установлено, что яв­ляется причиной, а что следствием. Статиче­ские заряды создают электрическое поле, в то время как движущиеся заряды — магнитное. Взаимосвязь электрического и магнитного по­лей со статическими и движущимися зарядами описывается уравнениями Максвелла. Вот о том, что представляет собой электромагнитное поле в автомобиле, мы и поговорим в этой статье.

 

 

Присутствие поля обнаруживается благо­даря его силовому воздействию на другие электрические заряды. Сила, воздействую­щая на точечный электрический заряд Q в электрическом поле, называется силой Кулона. Она вызывает отталкивание между одноименными зарядами и притяжение между разноименными. Сила, возникающая в вакууме между двумя точечными электрическими за­рядами Q₁ и Q₂ при расстоянии а между ними, равна:

F = Q₁·Q₂/4π·ε₀·a²

где:

ε_о=8,854-10^-12 Ф/м — эта электрическая по­стоянная, также называемая диэлектрической проницаемостью вакуума.

 

 

Сила, воздействующая на заряд, движу­щийся в магнитном поле, называется силой Лоренца. Она же является причиной взаимо­действия двух параллельных проводников, по которым протекают токи I₁ и I₂. Сила притя­жения в вакууме между двумя параллельными проводниками длиной l, расположенными друг от друга на расстоянии а, равна:

F = μ0·I₁·I₂ ·l/2π·a

где: μ_о=1,257 10^-6 Гн/м — это магнитная постоян­ная, также называемая магнитной проницае­мостью вакуума.

 

Электрическое поле

 

Сила, действующая на статический электри­ческий заряд, указывает на наличие элек­трического поля. Электростатическое поле описывается нижеследующими величинами.

 

Электрический потенциал φ(Р) и напряжение U

 

Электрический потенциал φ(Р) в точке Р- мера работы, требуемой для переноса заряда Q из исходной точки в точку Р:

φ(Р) = W(Р)/Q

Напряжение U- это разность потенциалов (от­носительно некоторой исходной точки) между двумя точками P₁ и Р₂:

U=φ(P₁)-φ(P₂)

 

Напряженность электрического поля Е

 

Напряженность электрического поля Е в точке Р зависит от ее положения в зоне дей­ствия заряда. Она описывается максимумом градиента потенциала в точке Р. Напряжен­ность электрического поля в точке, располо­женной на расстоянии а от положительного точечного заряда Q₁ равна:

E = Q₁ /4π·ε₀·a²

Вектор напряженности электрического поля направлен от положительного точечного за­ряда Q₁ На положительный заряд Q₂ в точке Р в том же направлении, что и вектор напряжен­ности электрического поля, действует сила:

F = Q₂ ·E

 

Электрическое поле и вещество

 

Электрическое поле в поляризованном (диэ­лектрическом) материале создает электриче­ский диполь (состоящий из положительного и отрицательного зарядов ±Q, расположенных на расстоянии а произведение Q·a называется дипольным моментом). Дипольный момент в единицу объема называется электрической поляризованностью М. Электрическое смещение D, означающее плотность электрического по­тока смещения, определяется по формуле:

D = εE = ε₀ε_rE = ε₀E + M

где:

ε = ε₀·ε_{r — диэлектрическая постоянная:}

ε₀— электрическая постоянная (диэлектрическая проницаемость вакуума):

ε_r — диэлектрическая постоянная (относительная диэлектрическая проницаемость).

Для воздуха ε_r =1; другие вели­чины см. в разделе «Изоляционные материалы».

Параметр

w_e = 1/2 ED

называется плотностью энергии электриче­ского поля. При ее умножении на объем полу­чаем электрическую энергию электрического поля W_e.

 

Конденсатор

 

Конденсатором называется устройство, состоящее из двух металлических тел (электродов), разде­ленных между собой диэлектриком (рис. «Устройство плоского конденсатора» ). При прикла­дывании к конденсатору напряжения, электроды заряжаются одинаково сильно, но разноименно. Полученный в результате заряд Q равен:

Q = CU

где С-емкость конденсатора. Она зависит от геометрической формы электродов, расстояния между ними и диэлектрической проницае­мости диэлектрика.

 

 

В таблице «Емкость C для проводников разного расположения» приведены емкости для разных типов конденсаторов и проводников с разным расположением. 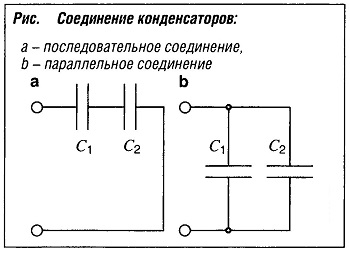Емкость конденсаторов при последовательном и параллельном соединении определяется по формулам:

1/C_total =  1/C₁ + 1/C₂ (последовательное соединение, рис. а, «Соединение конденсаторов» ),

C_total = С₁ + С₂ (параллельное соединение, рис. Ь, «Соединение конденсаторов» ).

На рис. 2 показан плоский конденсатор, со­стоящий из двух вставленных друг в друга конденсаторов, пластины которых соединены параллельно и действуют как электроды.

Энергия заряженного конденсатора (с за­рядом Q, напряжением U, емкостью С) равна:

W=1/2QU=Q²/2C=1/2CU²

 

Постоянный электрический ток и напряжение постоянного тока

 

Движущиеся заряды создают электрический ток, который характеризуется силой тока I, измеряемой в амперах. Для постоянного тока его направление и сила не зависят от времени. Электрическая система автомобиля, питается, с другой стороны, напряжением постоянного тока, которое также не зависит от времени. При этом электрический ток, протекающий в цепях системы электрооборудования автомобиля, обычно зависит от времени. Во многих случаях зависимый от времени электрический ток, как, на­пример постоянный ток, может быть управляем.

 

Направление электрического тока и его измерение

 

Направление электрического тока от поло­жительного полюса источника тока к отрица­тельному обозначается как положительное (в действительности 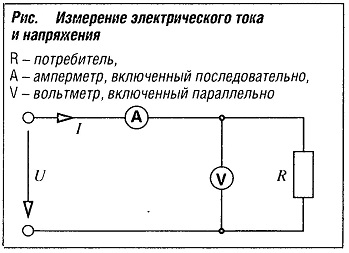электроны перемещаются от отрицательного полюса к положительному).

Измерение электрического тока производится амперметром (А), включенным в электрическую цепь последовательно; напряжение измеряется вольтметром (V), подключаемым параллельно тем точкам электрической цепи, напряжение между которыми надо измерить (рис. «Измерение электрического тока и напряжения» ).

Принятое направление электрического тока и напряжения показывается стрелкой. В соответствии с этой ориентацией, напря­жению и электрическому току присваивается знак. В случае положительного напряжения и электрического тока, стрелка указывает направление от положительного полюса (+) к отрицательному (-).

 

Закон Ома

 

Закон Ома описывает зависимость между напряжением U и силой тока в твердых и жидких электрических проводниках:

U=RI

Коэффициент пропорциональности R назы­вается омическим сопротивлением, которое измеряется в Омах (Ом). Величина, обратная сопротивлению, называется электрической про­водимостью G, измеряемой в Сименсах (См):

G=1/R

 

Омическое сопротивление

 

Омическое сопротивление материала зависит от его вида и размеров.

Для твердого провода:

R = ρl/q = l/qσ

где:

ρ — удельное сопротивление, Ом·мм²/м;

σ =1/ρ — электропроводность, м/(Ом·мм²);

l-длина провода, м;

q-площадь поперечного сечения провода, мм².

Для трубы (изнутри наружу):

R = ln(r₂/r₁)· 1/2π·l·σ

где:

l — длина трубы, м;

r₂, r₁— наружный и внутренний радиусы трубы, м.

Сопротивление металлов с повышением тем­пературы увеличивается:

R_T=R₂₀[1+a·(T-20 °С)]

где:

R_T — сопротивление при температуре Т;

R₂₀ — сопротивление при температуре 20 °С;

а-температурный коэффициент, [1/К] (=[1/°С]);

T-температура, [°С].

 

Работа и мощность

 

В резисторе, через который проходит элек­трический ток, совершается работа, которая за время t преобразуется в теплоту или другой вид энергии (с омическим сопротивлением R, напряжением U и силой тока I):

W = UIt=RI²t

При этом мощность равна:

Р= UI=RI²

 

Законы Кирхгофа

 

Первый закон Кирхгофа: закон электрического тока

Для каждой точки (узла) разветвления сумма втекающих электрических токов равна сумме вытекающих из этой точки электрических токов.

Второй закон Кирхгофа: закон напряжения

Для любого замкнутого контура разветвлён­ной цепи сумма всех падений напряжений на участках цепи равна сумме электродвижущих сил источников в этом контуре.

 

Электрические цепи постоянного тока

 

Цепь с потребителем

 

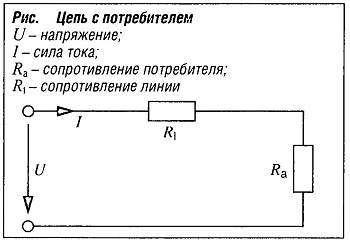
U=(R_a + R_l)I  

где:

R_a — омическое сопротивление потребителя;

R_l — сопротивление линии.

 

 

 

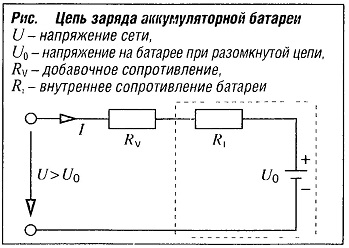
Цепь заряда аккумуляторной батареи

 

U-U₀ = (R_v + R_l)I 

где:

U — напряжение сети;

U₀ — напряжение на батарее при разомкнутой цепи (электродвижущая сила);

R_v — добавочное сопротивление;

R_l — внутреннее сопротивление батареи.

Условие заряда: U>U₀

 

Последовательное соединение резисторов

 

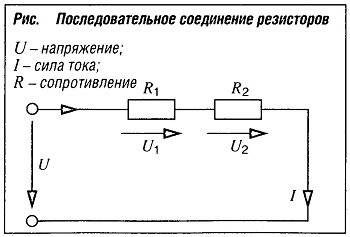
R_total = R₁ +R₂

U = U₁ +U₂

 

В обоих резисторах — одинаковая сила тока I (первый закон Кирхгофа).

 

1/R_total = 1/R₁ +1/R₂  или G_total = G₁ +G₂

 

Параллельное соединение резисторов

 

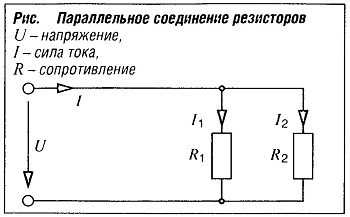
I = I₁+I₂ ; I₁/I₂ = R₁/R₂  

 

Напряжение U на всех резисторах одинаково (второй закон Кирхгофа).

 

Измерение сопротивления

 

Сопротивление можно установить измерением электрического тока или напряжения, а также не­посредственным измерением с использованием омметра или измерительного моста. 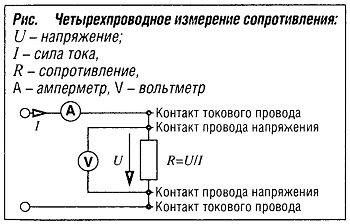Измеритель­ные мосты используются, например, в датчиках давления — при подключении тензодатчиков.

Широко используется четырехпроводный метод измерения сопротивления, особо малых значений (рис. «Четырехпроводное измерение напряжения» ). Для того чтобы пре­дотвратить погрешность из-за влияния пере­ходного сопротивления в точках подключения, используются две пары проводов. По одной паре на измеряемое сопротивление подается небольшой электрический ток. С помощью другой пары с измеряемого сопротивления на вольтметр подается падение напряжения. При подсоединении проводов к выводам из­меряемого двухполюсника токовые провода не касаются проводов напряжения, так что переходные сопротивления в местах контактов не включаются в измерительную цепь.

 

Переменный электрический ток

 

Зависимости, используемые при описании постоянного электрического тока и постоян­ного напряжения, также применимы в более или менее измененной форме и к переменным электрическому току и напряжению. В частно­сти, закон Ома и законы Кирхгофа могут при­меняться без изменений.

 

Заряд и разряд конденсатора

 

Когда электрический ток проходит через кондинсатор, его заряд Q изменяется:

I = dQ/dt

Таким образом, существует связь между си­лой тока I и напряжением U на конденсаторе емкостью С:

I = d(CU)/dt

В этом случае сила тока I подводится к пласти­нам конденсатора, имеющим заряд Q, между которыми существует напряжение U.

Примеры (емкость С постоянна с течением времени):

• напряжение постоянного тока U: —> сила тока I=0;

• напряжение начала разряда U₀  постоян­ная сила тока I: —> напряжение U=U₀+It;

• напряжение гармоническое (сину­соидальное), описываемое формулой U=û·sin(ωt): —> электрический ток косинусоидальный, описываемый формулой:  I=ω·C·û·cos(ωt) = ω·C·û·sin(ωt + π/2) , где:

ω=2πf  — угловая частота, зависящая от частоты f,

û — амплитуда напряжения.

Действующие значения и u_ff = û/√2 и i_eff = î /√2 также используются вместо амплитуд.

При протекании через конденсатор пере­менного (гармонического) электрического тока векторы электрического тока и напря­жения сдвинуты на угол φ = π/2. Это свойство иллюстрирует векторная диаграмма (рис. «Векторная диаграмма конденсатор» ).

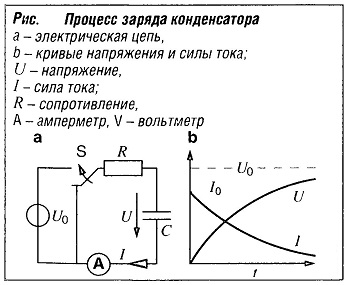
На рис. 10 показана электрическая цепь, в которой конденсатор заряжается через сопротивление, установленное со стороны источника напряжения постоянного тока U₀ (рис. «Процесс заряда конденсатора» ), или разряжается через сопротивление. Решающим фактором заряда и разряда конденсатора является постоянная времени τ=RC.

 

Процесс заряда 

 

I=(U₀/R)·e^—l/τ ; U = U₀ (1-e^—l/τ )

Процесс разряда

 

I=(U₀/R)·e^—l/τ ; U=U_0·e^—l/τ

где:

U₀-напряжение заряда или напряжения начала разряда;

I-зарядная или разрядная сила тока;

I₀= U₀/R — сила тока начала заряда;

R-зарядное или разрядное сопротивление;

U— напряжение на конденсаторе.

Зарядный и разрядный электрические токи противоположно направлены.

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: