Электрические двигатели в автомобиле — это электрические машины (электромеханические преобразователи), в которых электрическая энергия преобразуется в механическую. В основу работы подавляющего числа электрических машин положен принцип электромагнитной индукции. Вот о том, что представляют собой электрические двигатели, мы и поговорим в этой статье.

 

 

 

Систематика роторных электрических машин

 

Электрические двигатели в автомобиле являются электро-магнето-механическими преобразо­вателями энергии. При энергии W_m, имеющейся в магнитном поле, разряд, согласно углу вращения γ, создает магнитную силу F_t:

F_t = δ W_m / δ γ

Она служит тангенциальной силой для соз­дания крутящего момента, вычисляемого по радиусу ротора r (рис. «Принцип работы роторных электрических машин» ). Это можно описать выражением:

М = F_t r.

Электрические машины можно поделить на категории по их управлению (табл. «Систематический подход к электрическим двигателям»). Часть этой систематизации взята из стандарта DIN 42027.

 

 

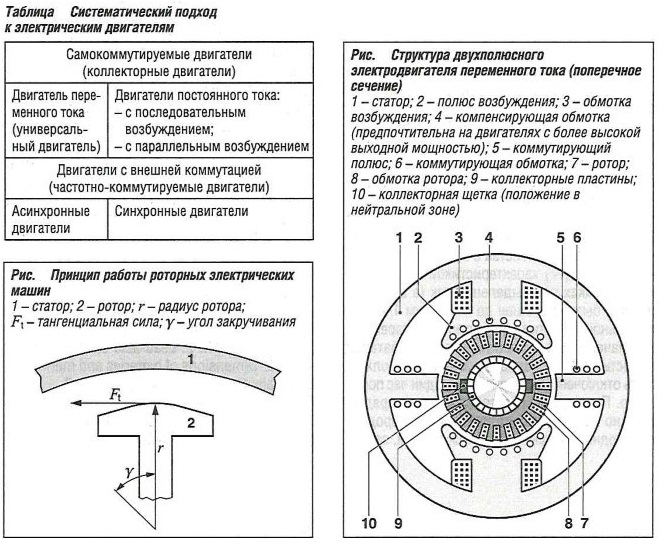
Двигатели постоянного тока

 

Для работы в качестве двигателей часто вы­бираются двигатели постоянного тока. Они ис­пользуются, например, в качестве приводов для электрических топливных насосов, вентилятор­ных электродвигателей, пусковых электродви­гателей, электродвигателей стеклоочистителей ветрового стекла и стеклоподъемников.

Двигатель постоянного тока (рис. «Структура двухполюсного эектродвигателя переменного тока» ) со­стоит из статора с возбуждающей, компенси­рующей и коллекторной обмотками, а также ротора (якоря) с роторной обмоткой. Ротор запитывается через коллекторные щетки и коллекторные пластины. Обмотки можно со­единять параллельно или последовательно.

Двигатели постоянного тока классифици­руются по различным характеристикам (с по­следовательным или параллельным возбуж­дением). Приведенные вычисления относятся к самокоммутирующимся двигателям. Схемы соединений двигателей постоянного тока регламентируются стандартом DIN EN 60034, часть 8.

 

Коммутация в двигателе постоянного тока

 

Для работы двигателя постоянного тока не­обходимо, чтобы направление тока в роторе оставалось постоянным относительно по­люсов статора (рис. «Принцип коммутации тока» ). 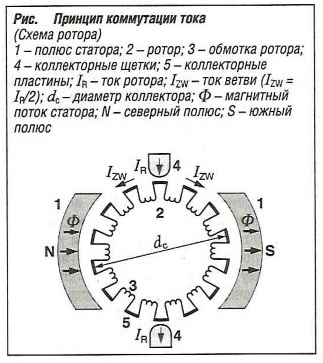Процесс изменения направления тока в роторе происходит в нейтральной зоне и называется коммута­цией. Коммутатор получает ток I_R через кол­лекторные щетки. Он делится на токи ветвей I_zw. Напряжение, наводимое в обмотках, вы­числяется по формуле:

u = -L d_i / d_t

Тангенциальная скорость v_t поверхности кол­лектора:

v_t = ω d_c / 2

Для определения длительности цикла Т_с учи­тывается количество коллекторных пластин:

Т_с = πd_c / v_t K

Изменение тока в коллекторной обмотке про­исходит за время Т_с. Если учесть, что имеет место лишь ток I_zw, то для наведенного на­пряжения применяется следующее:

u = -L (I_zw v_t K / πd_c)

Обозначения берутся из DIN 1304. часть 7.

 

Коммутирующая и компенсирующая обмотки

 

Распределение поля

 

Главное поле, беспрепятственно проникающее в ротор при отсутствии тока, имеет симметрич­ное распределение (рис. а, «Наложение полей» ). Аналогично, имеется симметричное разделение потока, когда ток подается только на ротор (рис. Ь, «Наложение полей» ).

При наложении этих полей нейтральная зона отклоняется на угол β (рис. с, «Наложение полей» ). Таким об­разом, эта магнитно-нейтральная зона больше не соответствует геометрически нейтральной зоне (положение коллекторных щеток).

 

 

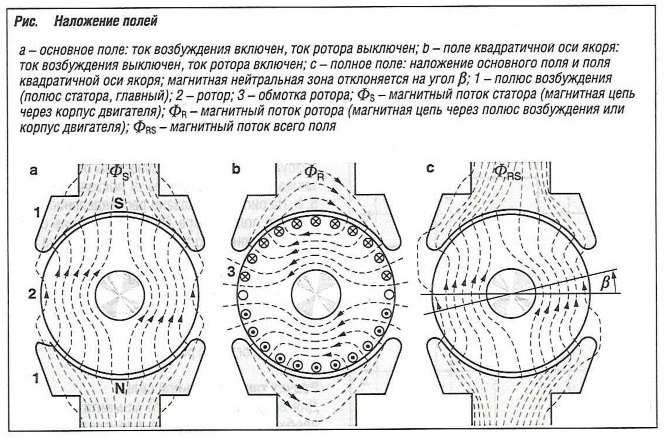
В геометрически нейтральной зоне это соз­дает магнитное поле, которое в процессе ком­мутации наводит напряжение в обмотке ротора, вызывая искрение между щеткой и движущейся коллекторной пластиной. Во избежание этого в процессе коммутации в этой обмотке наводится другое напряжение, где амплитуда и направле­ние компенсируют эффект изначально наведен­ного напряжения. Это достигается с помощью коммутирующей обмотки (рис. «Структура двухполюсного электродвигателя переменного тока» ). Коммутирую­щая обмотка последовательно подключается к обмотке ротора. Она использует обратную ре­акцию ротора для противодействия смещению в магнитно-нейтральной зоне.

В случае с двигателями без коммути­рующей обмотки щетки нужно смещать в магнитно-нейтральную зону. Возмущение основного поля, возникаю­щее в области полюсного башмака, ведет к снижению доступной поверхности клеммы вкупе с ростом магнитного сопротивления. Вот почему у более крупных двигателей име­ется компенсирующая обмотка, встроенная как полюсный башмак (рис. «Структура двухполюсного электродвигателя переменного тока» ). Компенсирующая обмотка последовательно соединяется с об­моткой ротора, и ее размеры таковы, чтобы компенсировать поперечное поле ротора.

 

Эффект коммутирующей и компенсирующей обмоток

 

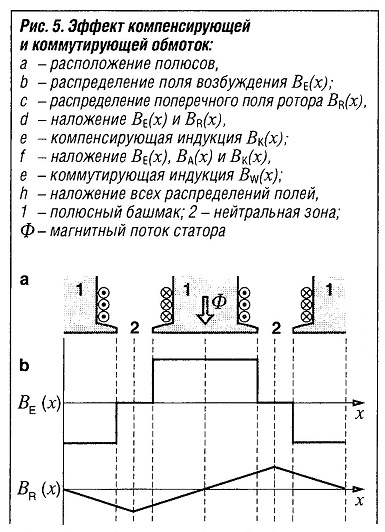
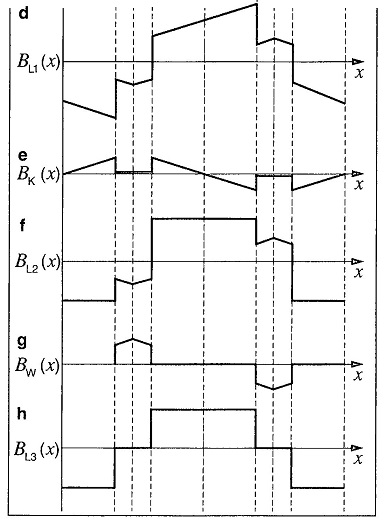
Последовательность изображений на рис. «Эффект компенсирующей и коммутирующей обмоток» описывает эффект обеих обмоток. Показаны распределения полей в воздушном зазоре. Рас­положение полюсов с обмоткой и нейтральной зоной показано на рис. а. Распределение поля возбуждения В_E(х) под полюсным башмаком, а также полюсное деление τ_Р показаны на рис. Ь. На рис. с показано распределение попе­речного поля ротора B_r(x). Наложение обоих распределений полей можно увидеть на рис. d. Компенсирующая индукция B_k(x) (рис.5е) и наложение из рис. d показаны на рис. f. Если коммутирующая индукция B_w(x) на рис. g накладывается на распределение поля из рис.  f, то получаем желаемое распределе­ние поля согласно рис. h.

 

Расчет тангенциальной силы ротора

 

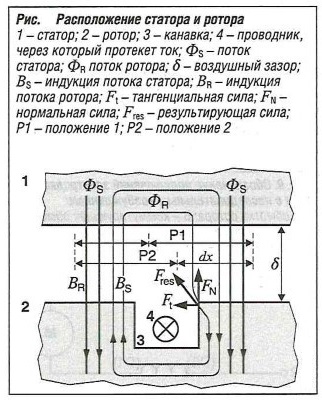Для создания крутящего момента на роторе необходима тангенциальная сила. Объекты исследования — статор и ротор с канавкой (рис. «Расположение статора и ротора» ), в которой находится токоведущий проводник (прядь обмотки). Ротор переме­щается из положения 1 в положение 2. Поток статора Ф_s создает индукцию B_s в воздуш­ном зазоре, а проводник в роторе, через ко­торый протекает ток, вызывает индукцию В_R. С левой стороны канавки образуется деструк­тивное, а с правой стороны — конструктивное наложение этих двух индукций. Энергия, на­копленная в воздушном зазоре с левой сто­роны канавки, равна:

dW2 = (δI_L/2μ₀) (B_s²-B_R²)dx       (уравнение 1).

С правой стороны канавки она равна:

dW1 = (δI_L/2μ₀) (B_s²+B_R²)dx            (уравнение 2).

Работа dW, выполняемая в этой части, по­лучается из разности между энергиями dW₁ и dW₂:

dW = dW1- dW₂ = F_t dx               (уравнение 3).

Уравнения 1, 2 и 3 можно использовать для вычисления силы F_t. Это можно описать вы­ражением:

F_t dx = (l_Rδ/2μ₀) [(B_s²-B_R²)-(B_s²+ B_R²)]dx.

Это значит, что:

F_t = (l_Rδ/2μ₀) B_R²

Магнитно-эффективная длина ротора равна l_R. Сила F_t  — это квадратичная функция ин­дукции провода, по которому протекает ток. Влияния индукции статора компенсируют друг друга. Поскольку силы на пограничных слоях всегда воздействуют в направлении низкой проницаемости, то они влияют на кру­тящий момент из-за потоков, возникающих по бокам от канавки.

 

Электродвигатель параллельного возбуждения

 

Особенностью электродвигателя параллель­ного возбуждения является то, что обмотка ротора параллельно соединяется с обмоткой возбуждения. 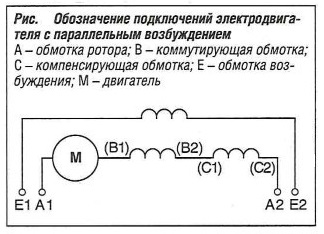Для электродвигателя парал­лельного возбуждения действуют следующие условия подключения (рис. «Обозначение подключений электродвигателя с параллельным возбуждением» ):

• А — обмотка ротора:
• А — коммутирующая обмотка;
• С — Компенсирующая обмотка;
• Е — обмотка возбуждения.

Расчет электродвигателя параллельного возбуждения базируется на сопротивлении ротора R_A и напряжении, наводимом обмот­кой ротора. Напряжение на клеммах U_Kl со­ставляется из напряжения ротора U_A = I_А R_A и наведенного напряжения U_ind = c₁ n Ф_S:

U_Kl = I_А R_A + c₁ n Ф_S  (уравнение 4).

Здесь с₁ обозначает конструктивно опреде­ляемую константу двигателя, зависящую от количества катушек в обмотке ротора, n — ча­стота вращения, Ф_S — поток статора, I_А — ток ротора.

Решение уравнения 4 для n дает скорость вращения (уравнение частоты вращения — тока ротора):

n = (- R_A /c₁Ф_S) I_А + U_Kl /c₁Ф_S  (уравнение 5).

Если момент двигателя М_м = с₂Ф_S I_Авставить в уравнение частоты вращения — тока ротора (уравнение 5), то получим уравнение частоты вращения — крутящего момента

n = (- R_A /c₁·с₂·Ф_S²) М_м + U_Kl /c₁·Ф_S  (уравнение 6).

с₂ — это тоже конструктивно определяемая константа двигателя, зависящая от количе­ства катушек в обмотке ротора.

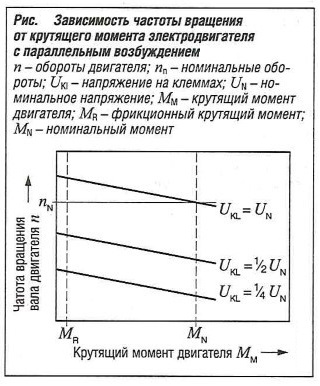На рис. «Зависимость частоты вращения от крутящего момента электродвигателя с параллельным возбуждением» показаны рабочие характеристики электродвигателя параллельного возбуждения. Для преодоления трения двигатель должен развивать фрикционный момент M_R. В момент включения частота вращения равна нулю. Это позволяет вычислить пуско­вой момент

M_A = U_Kl c₂Ф_S /R_A

в уравнении 6. При теоретически самой высо­кой частоте вращения на характеристической кривой (холостые обороты), двигатель не развивает крутящий момент. Холостые обо­роты n₀ равны

n₀ = U_Kl /c₁Ф_S

 

 

Электродвигатель с последовательным возбуждением

 

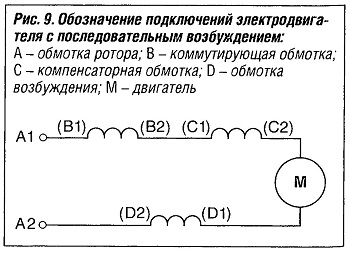У электродвигателя с последовательным воз­буждением коммутирующая, компенсирую­щая, возбуждающая обмотки статора и об­мотка ротора соединяются последовательно (рис. «Обозначение подключений электродвигателя с последовательным возбуждением» ). D обозначает обмотку возбуждения электродвигателя с последовательным воз­буждением. Чтобы определить рабочие характеристики, суммируем сопротивления обмоток, и получаем сопротивление R_A.

Точно таким же образом, как и в случае с электродвигателем параллельного возбуж­дения, напряжение на клеммах U_KL склады­вается из напряжения ротора и наведенного напряжения:

U_Kl = I_А R_A + c₁ n Ф_S                         (уравнение 7).

В результате получаем уравнение скорости вращения:

n = (- R_A /c₁Ф) I_А + U_Kl /c₁Ф_S   (уравнение 8).

Магнитный поток можно вычислить с помо­щью другой константы двигателя с₃:

Ф = с₃ I_А                                             (уравнение 9).

Константа двигателя с₃ имеет единицу ин­дуктивности и поэтому зависит от геометрии, количества катушек и проницаемости. Крутя­щий момент двигателя М_м вычисляется по формуле

М_м = с₂с₃I_А²                                    (уравнение 10).

Если уравнение 10 скорректировать согласно I_А, это выражение будет действительно в уравнении 9 и оно, в свою очередь, в уравне­нии частоты вращения — тока (уравнение 8). В результате получаем:

n =  (- R_A/c₁·с₃) +  (U_Kl √с₂·с₃/с₁·с₃) (1/√М_м )  (уравнение 11).

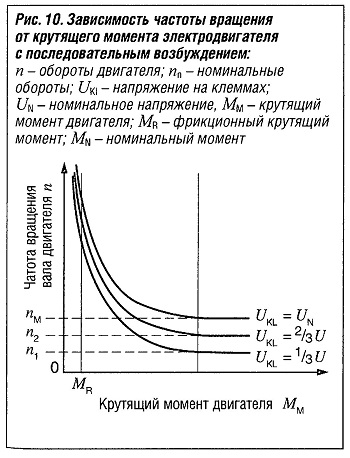
В отличие от электродвигателя с параллель­ным возбуждением, здесь частота вращения пропорциональна соответствующему значе­нию корня крутящего момента (рис. «Зависимость частоты вращения от крутящего момента электродвигателя с последовательным возбуждением» ). Дви­гатель характеризуется значительным паде­нием частоты вращения при малой нагрузке. Если внешняя нагрузка на двигатель будет равна нулю, то частота вращения теоретиче­ски будет стремиться к бесконечности.

 

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ: