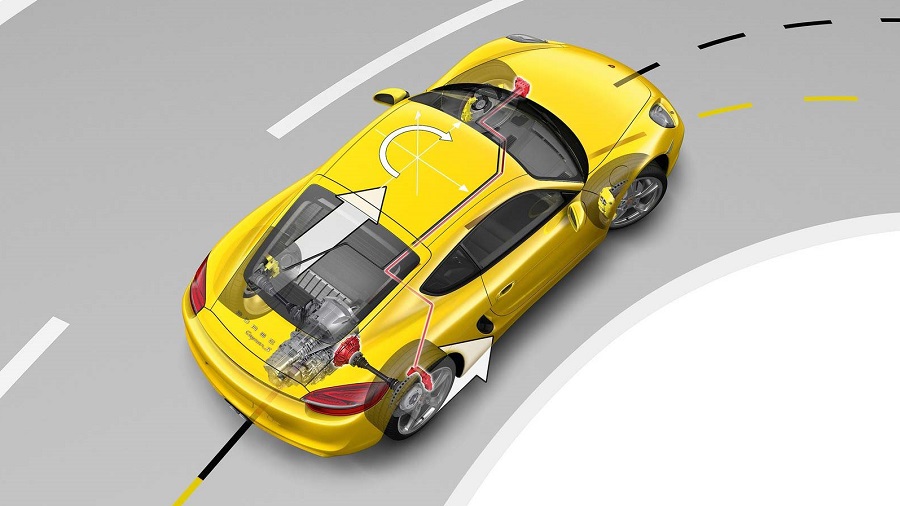
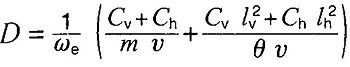На страницах этого справочник мы уже неоднократно упоминали о динамике поперечного перемещения автомобиля. От того, как автомобиль может сопротивляться поперечному перемещению, во многом зависит его поведение на дороге. В этой статье мы подробно поговорим, что представляет собой динамика поперечного перемещения автомобиля.

 

 

Диапазоны бокового ускорения

 

На современных легковых автомобилях бо­ковое ускорение может достигать 10 м/с². Величина бокового ускорения разделяется на следующие диапазоны (рис. «Диапазоны бокового ускорения» ):

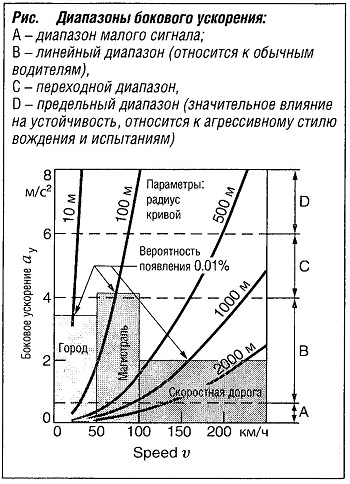Диапазон от 0 до 0,5 м/с² известен под на­званием диапазона малого сигнала. В этом диапазоне явление возникает при прямоли­нейном движении под действием таких воз­мущений, как неровности дороги и боковой ветер. Ветровые возмущения возникают вследствие порывов ветра и при въезде в за­крытые от ветра зоны и выезде из них.

Диапазон от 0,5 до 4 м/с² известен под на­званием линейного диапазона, поскольку по­ведение автомобиля в этом диапазоне может быть описано при помощи линейной, одноколейной модели. К типичным маневрам, свя­занным с динамикой поперечного движения, относятся резкое манипулирование рулем, пе­рестроения из ряда в ряд, а также комбинации маневров, связанных с изменением динамики как продольного, так и поперечного движения, например, вследствие реакций на изменения нагрузки при прохождении поворотов.

В диапазоне бокового ускорения от 4 до 6 м/с², в зависимости от конструктивных особенно­стей автомобиля, его поведение в отношении бокового ускорения может оставаться линей­ным или становиться нелинейным. Поэтому этот диапазон рассматривается как переход­ной. В этом диапазоне автомобили с макси­мальным боковым ускорением от 6 до 7 м/с² (например, внедорожные автомобили) уже демонстрируют нелинейные характеристики, в то время как автомобили, достигающие более высоких уровней бокового ускорения (напри­мер, спортивные автомобили) продолжают показывать линейные характеристики.

Боковое ускорение свыше 6 м/с² достигается только в экстремальных ситуациях, поэтому рассматривается как предельный диапазон. В этом диапазоне характеристики автомобиля в основном нелинейные и оказывают влияние на устойчивость автомобиля. Этот диапазон достигается на спортивных трассах или в си­туациях, в условиях обычного дорожного дви­жения приводящих к авариям.

Для среднего водителя боковое ускорение обычно составляет до 4 м/с². Это означает, что при субъективной оценке ситуации водитель управляет автомобилем таким образом, что бо­ковое ускорение находится в диапазоне малого сигнала или в границах линейного диапазона (рис. Диапазоны бокового ускорения). Для среднего водителя вероятность возникновения бокового ускорения экспонен­циально снижается с падением скорости.

 

Одноколейная линейная модель

 

Из одноколейной линейной модели могут быть получены важные выводы, касающиеся дина­мических характеристик поперечного движе­ния. В одноколейной линейной модели динами­ческие свойства одной оси и ее колес сведены в одно эффективное колесо. В простейшем ва­рианте, как показано здесь, рассматриваемые характеристики находятся в линейном диапа­зоне, что объясняет, почему модель этого типа называется одноколейной линейной моделью. Наиболее важными модельными предположе­ниями являются следующие:

• Кинематика и эластокинематика оси моде­лируются только линейно;
• Поперечная сила, действующая на шину, возрастает линейно, а стабилизирующий крутящий момент игнорируется;
• Предполагается, что центр тяжести автомо­биля находится на уровне дороги. Следова­тельно, единственной вращательной степе­нью свободы автомобиля является движение рыскания. Крен, продольная качка и под­скоки на неровностях не учитываются.

 

 

Способность автомобиля к восстановлению прямолинейного движения

 

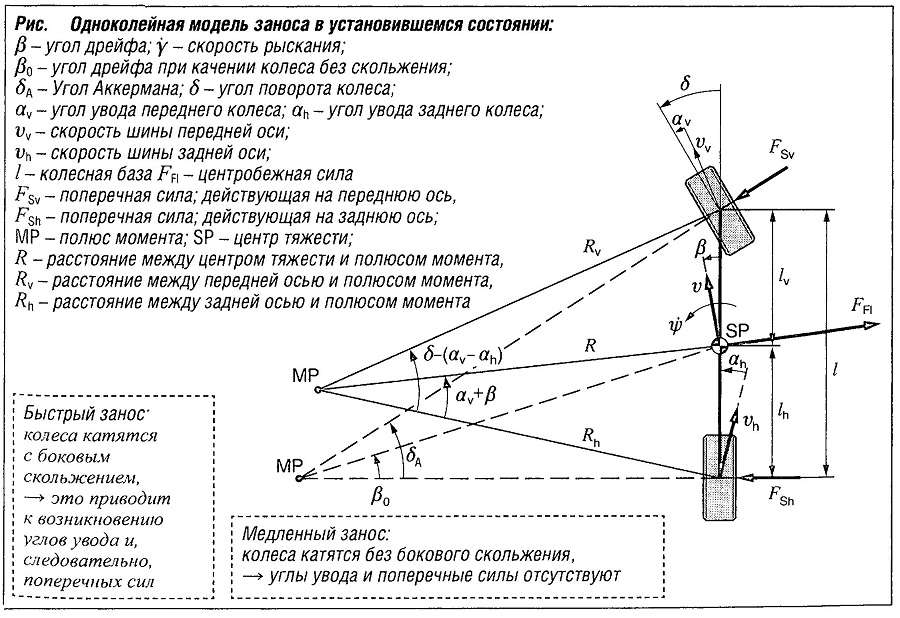
На рис. «Одноколейная модель заноса в установившемся состоянии» представлена однолинейная модель для условий быстрого и медленного заноса. Результатом этого представления являются следующие соотношения, описывающие ки­нематику углов скольжения:

a_v = δ — β — (Ψ ⋅ l_v)/v

a_h = — β — (Ψ ⋅ l_h)/v

Вместе с балансом моментов можно вычислить изменение угла поворота рулевого колеса, свя­занное с увеличением бокового ускорения, в условиях маневра с заносом при постоянном радиусе. Это дает определение градиента самовыравнивания управляемых колес EG:

EG = dδ/da_v = m/l⋅(l_h/C_v — l_v/C_h)

Конструкция всех легковых автомобилей в линейном диапазоне бокового ускорения предусматривает недостаточную поворачиваемость. Значение EG для легковых авто­мобилей составляет около 0,25 градус⋅с²/м.

В отношении динамики бокового движения градиент самовыравнивания управляемых колес характеризует устойчивость и демпфирование автомобиля. Кроме того, значение градиента самовыравнивания для среднего водителя стано­вится очевидным, поскольку угол поворота колес увеличивается с ростом скорости прохождения поворота. Это привлекает внимание водителя к возрастающему боковому ускорению.

Градиент угла дрейфа (SG) можно вычислить, воспользовавшись схемой, представленной на рис. «Одноколейная модель заноса в установившемся состоянии». В целях повышения устойчивости авто­мобиля градиент угла дрейфа должен быть как можно меньше.

SG = dβ/da_y = ml_v/C_hl

 

Коэффициент усиления рыскания

 

Коэффициент усиления рыскания опреде­ляет степень рыскания автомобиля в ответ на изменение угла поворота рулевого колеса в квазиустойчивом состоянии. Коэффициент усиления рыскания можно определить, вы­полнив следующее испытание: при движении с постоянной скоростью рулевое колесо по­ворачивается из стороны в сторону с частотой менее 0,2 Гц. Амплитуда угла поворота рулевого колеса выбирается таким образом, чтобы мак­симальное боковое ускорение составило около 3 м/с². Начиная со скорости 20 км/ч, маневр повто­ряется с увеличением скорости каждый раз на 10 км/ч. 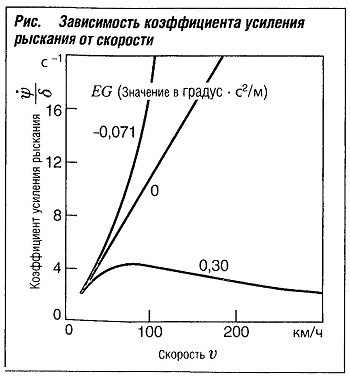При условии отсутствия аэродинамических воздействий на высоких скоростях (подъемных сил, воздействующих на переднюю и заднюю оси), результаты испытания дают кривые коэф­фициента усиления рыскания, в основном согла­сующиеся со следующим уравнением, выведен­ным из одноколейной линейной модели:

(Ψ/δ)_stat = v/(l+EG⋅v²)

На рис. «Зависимость коэффициента усиления рыскания от скорости» показан коэффициент усиления ры­скания для автомобиля, имеющего тенденцию к избыточной поворачиваемости (EG<0), нейтральную управляемость (EG=0) и тен­денцию к недостаточной поворачиваемости (EG>0). При высоких скоростях движения приемлемой является только недостаточная поворачиваемость, обеспечивающая тре­буемую динамику автомобиля даже во время движения по прямой. Скорость, при которой автомобиль, имеющий тенденцию к недо­статочной поворачиваемости, демонстрирует максимальную реакцию рыскания, известна как характеристическая скорость v_char. В ли­нейной одноколейной модели эта скорость выражается как:

v_char = √¯l/EG

 

Коэффициент демпфирования

 

Из линейной одноколейной модели выведено следующее уравнение равновесия сил:

тa_у = F_sv cos δ+F_sh.

Для баланса моментов:

Θψ = F_sv l_v cos δ + F_sh l_h

Коэффициент демпфирования D возмущения в отношении динамики поперечного движения может быть выведен из двух следующих уравнений:

Недемпфированная собственная частота вы­ражается следующим уравнением:

Коэффициент демпфирования автомобиля может быть определен, например, из реакции рыскания на резкий поворот рулевого колеса или иное ступенчатое входное воздействие. При разработке конструкции автомобиля раз­работчики стремятся получить как можно бо­лее высокий коэффициент демпфирования.

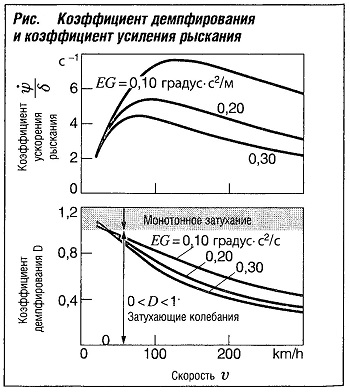
На рис. «Коэффициент демпфирования и коэффициент рыскания» показаны коэффициенты демп­фирования и усиления рыскания для различ­ных градиентов самовыравнивания. При этом имеет место следующий конфликт целей:

• если автомобиль должен обладать хоро­шими характеристиками прямолинейного движения, требуется высокое значение градиента самовыравнивания;
• для обеспечения высокого коэффициента демпфирования, особенно на высоких ско­ростях, градиент самовыравнивания дол­жен быть как можно более низким.

 

Диаграмма боковой подвижности автомобиля

 

Еще одной важной переменной, определяю­щей сбалансированность автомобиля, явля­ется общее передаточное отношение рулевого механизма i_l. Угол поворота рулевого колеса i_l вычисляется, исходя из угла поворота оси, как:

δ_H =i_l ⋅ δ

Это дает следующее уравнение для макси­мального коэффициента усиления рыскания:

(ψ/δ_H)_max = 1/2i_l√‾l⋅EG

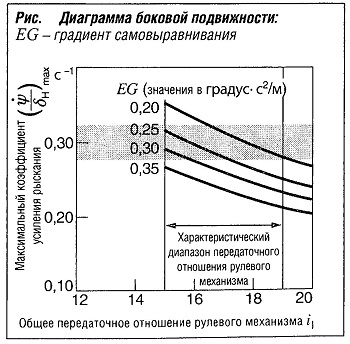Этот максимум построен на диаграмме бо­ковой подвижности (рис.»Диаграмма боковой подвижности» ) в функции пере­даточного отношения рулевого механизма. Дополнительно на диаграмме показаны изо­линии EG. Вдоль этих кривых градиент само­выравнивания постоянен. На этой диаграмме могут быть построены желаемые диапазоны коэффициента усиления рыскания и пере­даточного отношения рулевого механизма с Целью определения необходимых градиентов самовыравнивания.

Если в автомобиле изменяется только пе­редаточное отношение рулевого механизма, максимальный коэффициент усиления ры­скания можно определить при помощи диа­граммы боковой подвижности, сдвигая базо­вую линию вдоль изолиний EG. Если имеет место изменение характеристик оси, сдвиг осуществляется вдоль вертикальной оси.

 

Динамика поперечного движения автомобиля

 

Ветер может вызывать динамические эффекты в боковом направлении. Реакция автомобиля на эти внешние воздействия проявляется в виде отклонения от желаемой траектории дви­жения, бокового ускорения и изменения углов рыскания и крена. Чтобы противодействовать этим изменениям, водитель пытается вы­полнить корректирующие действия. Следова­тельно, необходимо учитывать скорость реак­ции водителя, а также способность автомобиля к коррекции. Согласно результатам исследова­ния, непосредственная реакция автомобиля на боковой ветер является основной переменной величиной для субъективной оценки общей устойчивости автомобиль под действием бо­кового ветра. Это дает преимущество, заклю­чающееся в том, что реакцию автомобиля на боковой ветер можно эффективно оценить посредством анализа.

Характеристически средний водитель вос­принимает два состояния, вызываемые возмущениями в виде бокового ветра:

• Естественный ветер, направление и ско­рость которого могут изменяться во время движения;
• Въезд и выезд из областей «ветровой тени», когда на автомобиль могут воздействовать силы, значительно изменяющиеся по величине.

 

В автомобилестроении стремятся свести к минимуму эффекты возмущений, вызываемых ветровыми нагрузками, учитывая следующие факторы:

• «Жесткость в повороте» шин, т.е. степень изменения поперечной силы при увеличении угла увода. При этом считается, что нагрузка на колесо остается постоянной;
• Общая масса автомобиля;
• Положение центра тяжести автомобиля;
• Характеристики оси;
• Симметричность и упругость подвески;
• Демпфирование;
• Кинематика и эластокинематика осей;
• Аэродинамическая форма и площадь лобовой поверхности автомобиля.

 

Аэродинамические силы и моменты

 

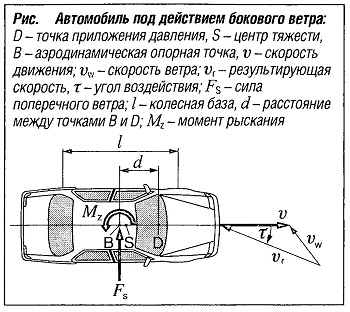
Когда автомобиль движется со скоростью v при ветре, имеющем скорость v_w, на него воздействует ветер с результирующей скоростью v_r. При наличии бокового ветра угол воздействия τ в общем случае отличен от 0 градусов, что приводит к возникновению поперечной силы F_s и момента рыскания М_z, воздействующих на автомобиль.

В аэродинамике стандартной практикой является указание вместо сил и моментов безразмерных коэффициентов. Отсюда:

F_s = (c_s ρ/2) v_r²A,

M_z = (c_M ρ/2) v_r²A l

Момент М_z и поперечная сила Fs, определенные в средней точке колесной базы, могут быть представлены единой поперечной силой F_s, когда точка приложения воздействия совпадает с точкой приложения давления D (рис. «Автомобиль под действием бокового ветра» ). Расстояние d между аэродинамической опорной точкой В и точкой приложения давления D вычисляется следующим образом:

d = M_z/F_s = c_Ml/c_s

Чтобы в максимальной степени уменьшить влияние аэродинамических эффектов, следует принять меры к тому, чтобы точка приложения давления D находилась как можно ближе к центру тяжести автомобиля. Это существенно снизит эффективное влияние момента.

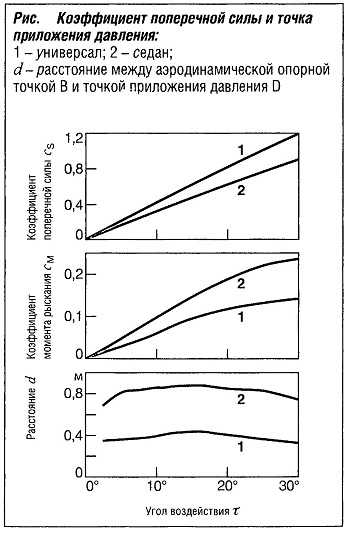
На рис. «Коэффициент поперечной силы и точка приложения давления» представлены аэродинамические коэффициенты для двух наиболее типичных кузовов автомобиля, универсала и седана, в функции угла воздействия τ. Результирующее расстояние d для универсалов значительно меньше, чем для седанов (см. рис. «Автомобиль под действием бокового ветра» ). Для автомобилей с центром тяжести, расположенным посередине колесной базы, конструкция универсала, следовательно, менее чувствительна к боковому ветру, чем у седана.

Поведение в повороте

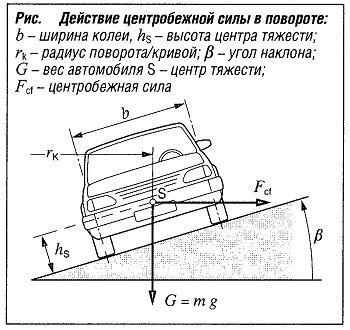
Центробежная сила, действующая в повороте (рис. «Действие центробежной силы в повороте» ):

F_cf = mv² / r_k

 

Боковой крен кузова в повороте

 

При движении в повороте центробежная сила, приложенная в центре тяжести автомобиля,    наклоняет кузов. Величина крена зависит от упругих характеристик подвески и ее воспри­имчивости к деформации, а также от плеча действия центробежной силы (расстояние между осью крена и центром тяжести авто­мобиля). Ось крена является одновременно мгновенной осью вращения кузова относи­тельно поверхности дороги. Подобно всем жестким телам, кузов автомобиля подверга­ется совместному воздействию на него скру­чивающих и поворачивающих усилий, усу­губляющих крен; это движение дополняется боковым смещением вдоль мгновенной оси.

Чем ближе расположена ось крена к центру тяжести автомобиля, тем выше его попереч­ная устойчивость и меньше крен при движе­нии в повороте. Однако обычно это вызывает соответствующее перемещение вверх колес, что приводит к изменению колеи и оказывает негативное влияние на безопасность дви­жения. Поэтому следует стремиться к тому, чтобы высокое расположение мгновенного центра крена сочеталось с минимальными изменениями колеи автомобиля. Таким об­разом, целью конструкторов является рас­положение мгновенных осей наклонов колес как можно выше относительно кузова и одно­временно как можно дальше от него.

 

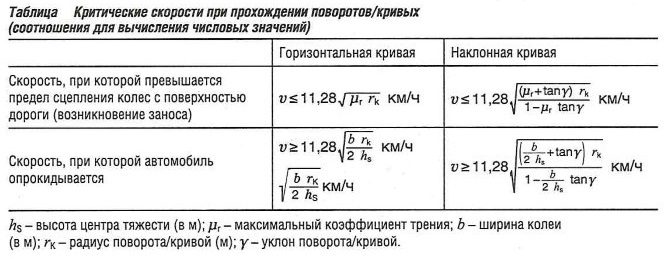
Таблица «Критические скорости при прохождении поворотов»

 

 

Часто для нахождения (приблизительного) оси крена определяются центры вращения (цен­тры крена) так называемого эквивалентного кузова. При этом рассматривают перемещение кузова в двух вертикальных относительно до­роги плоскостях, проходящих через переднюю и заднюю оси автомобиля. Центры крена — это те гипотетические точки на кузове, которые остаются неподвижными при крене. Ось крена, в свою очередь, представляет собой линию, соединяющую эти точки. Графическое пред­ставление центров крена базируется на правиле, согласно которому мгновенные центры враще­ния трех систем в состоянии относительного движения лежат на одной линии.

Сложность операций, требующихся для более точного определения пространствен­ных соотношений, описывающих движение колеса, делает целесообразным использова­ние трехмерной модели.